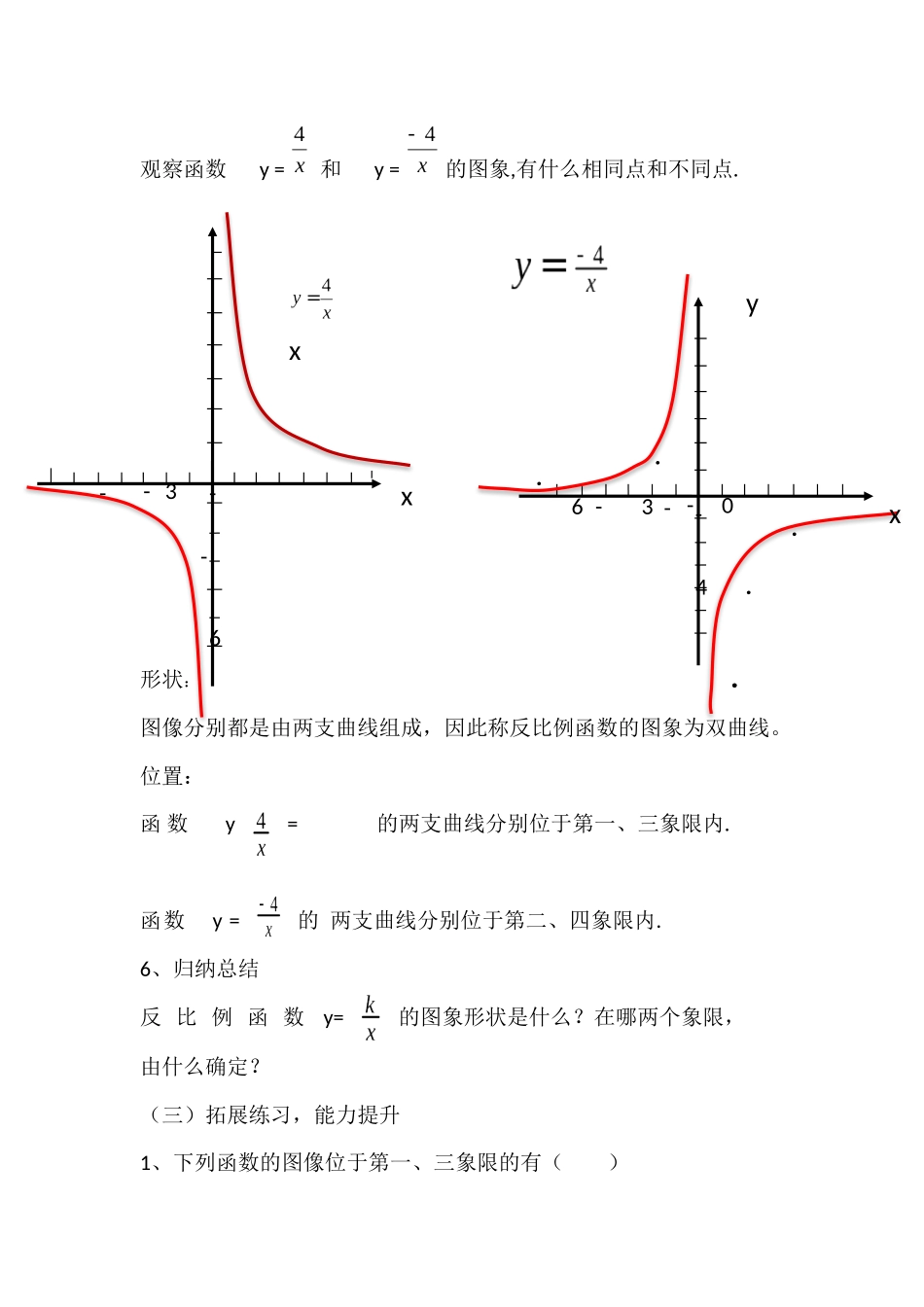
一、学习目标:1、学会在平面直角坐标系中用描点法画出反比例函数的图象。2、理解会用反比例函数的性质解答问题。3.培养观察分析问题的能力。4.体会由“特殊到一般”的数学思想和方法。二、学习过程(一)知识回顾:1.什么是反比例函数?反比例函数表达式有几种?2.画函数图像的一般步骤是什么?(二)探索新知1、合作探究例1.画出函数y=的图象。(查找问题、互学提高)展示学生画的函数图像,让学生查找不足。2、总结提升你认为作反比例函数图象时应注意哪些问题?3、观摩巩固观看y=正确的画图过程,巩固画图的步骤、方法4.画出函数y=的图象5、认真观察、总结特征观察函数y=和y=的图象,有什么相同点和不同点.形状:图像分别都是由两支曲线组成,因此称反比例函数的图象为双曲线。位置:函数y=的两支曲线分别位于第一、三象限内.函数y=的两支曲线分别位于第二、四象限内.6、归纳总结反比例函数y=的图象形状是什么?在哪两个象限,由什么确定?(三)拓展练习,能力提升1、下列函数的图像位于第一、三象限的有()-3---6xxxy....0-3--6.-4(1)y=(2)y=(3)y=(4)y=2、反比函数y=的图像在()A.第一、三象限B.第一、二象限C.第二、四象限D.第三、四象限(四)知识回顾(五)课堂检测1反比例函数y=的图象经过点(-1,2),k的值是()A.-1B.1C.-2D.22、函数y=(k≠0)的图象过点(2,-2),则此函数的图象在()A.第一、三象限B.第三、四象限C.第一、二象限D.第二、四象限3、若反比例函数y=的图象在第一、三象限则有()A.k≠0B.k≠3C.k<3D.k>34.若函数y=是反比例函数,且它的图象在二、四象限内,则n的值是()A.0B.1C.0或1D.3(六)作业