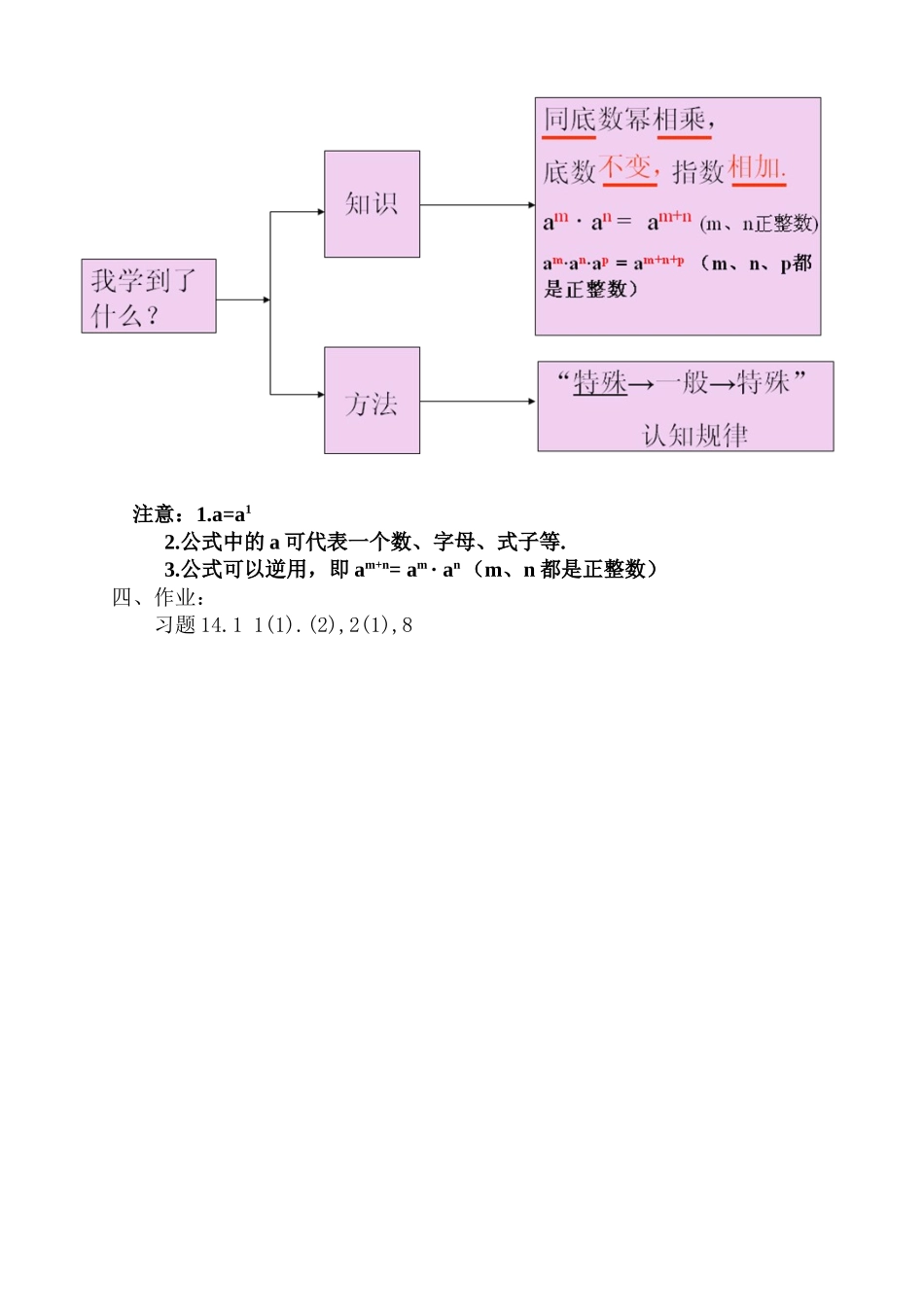
14.1.1同底数幂的乘法教学目标1、理解同底数幂的乘法法则2、运用同底数幂的乘法法则解决一些实际问题教学重点正确理解同底数幂的乘法法则教学难点正确理解和应用同底数幂的乘法法则教学过程一、提出问题,创设情景:an表示的意义是什么?其中a、n、an分别叫做什么?问题:1.25表示什么?2.10×10×10×10×10可以写成_________________形式二、讲授新课探究:式子103×102的意义是什么?这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.103×102=(10×10×10)×(10×10)=_______=10()23×22==________=2()a3×a2==_________=a().思考:请同学们观察下面各题左右两边,底数、指数有什么关系?103×102=10()23×22=2()a3×a2=a()猜想:am·an=?(m、n都是正整数)归纳:同底数幂的乘法性质:am·an=am+n(m、n都是正整数)同底数幂相乘,底数,指数。运算形式:(同底、乘法)运算方法:(底不变、指加法)如43×45=43+5=48想一想:当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?怎样用公式表示?am·an·ap=am+n+p(m、n、p都是正整数)例题引领例1.计算:(1)107×104.(2)x2·x5.(3)a·a6(4)(-2)6·(-2)8(5)xm·x2m+1(6)-26·(-2)8注意:1.a=a1例2.计算:(1)23×24×25(2)y·y2·y3练一练,我能行1.口答:(1)105×106(2)a7·a3(3)x5·x5(4)b5·b2.计算:(1)x10·x(2)10×102×104(3)x5·x·x3(4)y4·y3·y2·y3.下面的计算对不对?如果不对,怎样改正?(1)b5·b5=2b5()(2)b5+b5=b10()(3)x5·x5=x25()(4)y5·y5=2y10()(5)c·c3=c3()(6)m+m3=m4()变式训练填空:(1)x5·()=x8(2)a·()=a6(3)x·x3()=x7(4)xm·()=x3m合作、探究:1.计算:(1)—a(—a)4(—a)3(2)(x+y)3·(x+y)4(3)若ax=3,ay=2,则ax+y的值是多少?注意:2.公式中的a可代表一个数、字母、式子等.3.公式可以逆用,即am+n=am·an(m、n都是正整数)2.填空:(1)8=2x,则x=;(2)3×27×9=3x,则x=.挑战平台1、计算(1)35(—3)3(—3)2(2)xn·xn+1(3)xp(—x)2p(—x)2p+1(p为正整数)(4)32×(—2)2n(—2)(n为正整数)2、计算(1)(2a+b)3(2a+b)m-4(2a+b)2n+1(2)(x—y)2(y—x)5三、小结注意:1.a=a12.公式中的a可代表一个数、字母、式子等.3.公式可以逆用,即am+n=am·an(m、n都是正整数)四、作业:习题14.11(1).(2),2(1),8学案温故知新:an表示的意义是什么?其中a、n、an分别叫做什么?an=1.25表示什么?2.10×10×10×10×10可以写成_________________形式探究:式子103×102的意义是什么?这个式子中的两个因式有何特点?请同学们先根据自己的理解,解答下列各题.103×102=(10×10×10)×(10×10)=_________=10()23×22==______=2()a3×a2==__________=a().思考:请同学们观察下面各题左右两边,底数、指数有什么关系?103×102=10()23×22=2()a3×a2=a()猜想:am·an=?(m、n都是正整数)归纳:同底数幂的乘法性质:(m、n都是正整数)同底数幂相乘,底数,指数。练一练,我能行1.口答:(1)105×106(2)a7·a3(3)x5·x5(4)b5·b2.计算:(1)x10·x(2)10×102×104(3)x5·x·x3(4)y4·y3·y2·y3.下面的计算对不对?如果不对,怎样改正?(1)b5·b5=2b5()(2)b5+b5=b10()(3)x5·x5=x25()(4)y5·y5=2y10()(5)c·c3=c3()(6)m+m3=m4()变式训练填空:(1)x5·()=x8(2)a·()=a6(3)x·x3()=x7(4)xm·()=x3m合作、探究:1.计算:(1)—a(—a)4(—a)3(2)(x+y)3·(x+y)4(3)若ax=3,ay=2,则ax+y的值是多少?2.填空:(1)8=2x,则x=;(2)3×27×9=3x,则x=.挑战平台1、计算(1)35(—3)3(—3)2(2)xn·xn+1(3)xp(—x)2p(—x)2p+1(p为正整数)(4)32×(—2)2n(—2)(n为正整数)2、计算(1)(2a+b)3(2a+b)m-4(2a+b)2n+1(2)(x—y)2(y—x)5