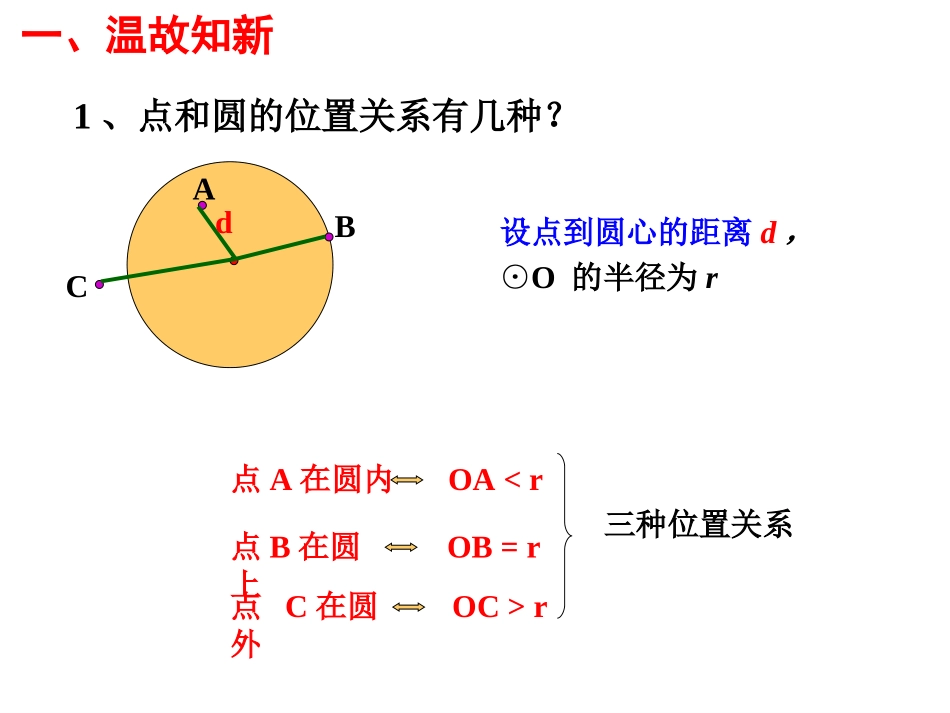
(第一课时)ABC1、点和圆的位置关系有几种?点A在圆内点B在圆上点C在圆外d设点到圆心的距离d,三种位置关系⊙O的半径为r一、温故知新OAr2、如图,O是直线l外一点,A、B、C、D是直线l上的点,且OD⊥l线段的长度是点O到直线l的距离。OD一、温故知新一、温故知新3、在下图画出点P到直线AB的垂线段。PBA地平线你发现这个自然现象反映出直线和圆的公共点的个数有种情况。三种如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线与圆的公共点的个数想象一下,直线和圆的位置关系有几种?二、新授讲解直线和圆没有公共点,这时我们就说这条直线和圆相离思考:一条直线和一个圆,如果有公共点能不能多于两个呢?相离相交相切切点切线割线交点交点直线和圆有两个公共点,这时我们就说这条直线和圆相交,这条直线叫做圆的割线直线和圆有且只有一个公共点,这时我们就说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.直线与圆交点的个数可以判断它们的关系1、直线与圆相离、相切、相交的定义。①从位置上看快速判断下列各图中直线与圆的位置关系.Ol.O1.Ol.O2ll..1)2)3)4)相交相切相离直线l与O1相离直线l与O2相交O(从直线与圆公共点的个数)●●●●●学以致用•直线和圆相交dr;dr;直线和圆相切直线和圆相离dr;直线与圆的位置关系量化●O●O相交●O相切相离rrr┐dd┐d┐<=>②从数量上看:lll归纳判定直线与圆的位置关系的方法有两种:(1)根据定义,由直线与圆的公共点的个数来判断;(2)由圆心到直线的距离d与半径r的大小关系来判断。在实际应用中,常采用第二种方法判定3)若AB和⊙O相交,则.22、已知⊙O的半径为6cm,圆心O与直线AB的距离为d,根据条件填写d的范围:1)若AB和⊙O相离,则;2)若AB和⊙O相切,则;d>6cmd=6cmd<6cm0cm≤小练习1..直线和圆有直线和圆有22个交点个交点,,则直线和圆则直线和圆_________;_________;直线和圆有且只有直线和圆有且只有11个交点个交点,,则直线和圆则直线和圆____;____;直线和圆有没有交点直线和圆有没有交点,,则直线和圆则直线和圆_________;_________;相交相交相切相切相离相离直线与圆的位置关系表格演示直线与圆的位置关系相交相切相离公共点个数公共点名称直线名称图形圆心到直线距离d与半径r的关系dr2交点割线1切点切线0AlO请在⊙O上任意取一点A,连接OA。过点A作直线l⊥OA。思考一下问题:1.圆心O到直线l的距离和圆的半径有什么数量关系?2.二者位置有什么关系?为什么?3.由此你发现了什么?lA探究发现:(1)直线l经过半径OA的外端点A;(2)直线l垂直于半径0A.则:直线l与⊙⊙OO相切相切这样我们就得到了从几何角度上来判定直线是圆的切线的方法——切线的判定定理.AOl2.直线与圆相切的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线。对定理的理解:切线需满足两条:①经过半径外端;②垂直于这条半径.OOrrllAA OAOA是半径,是半径,ll⊥OA⊥OA于点于点AA∴∴ll是⊙是⊙OO的切线。的切线。定理的几何符号表达定理的几何符号表达::判断对错1.过半径的外端的直线是圆的切线()2.与半径垂直的的直线是圆的切线()3.过半径的端点与半径垂直的直线是圆的切线()××××××OOrrllAAOOrrllAAOOrrllAA利用判定定理时,要注意直线须具备以下两个条件利用判定定理时,要注意直线须具备以下两个条件,,缺一不可缺一不可(1)(1)直线经过半径的外端直线经过半径的外端;;(2)(2)直线与这半径垂直。直线与这半径垂直。问题:定理中的两个条件缺少一个行不行?•切线的判定方法有三种:•①直线与圆有唯一公共点;•②直线到圆心的距离等于该圆的半径;•③切线的判定定理.即•经过半径的外端并且垂直这条半径的直线是圆的切线判定直线与圆相切有哪些方法?方法小结〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。OOBBAACC分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可。证明:连结OC(如图)。 ⊿OAB中,OA=OB∴⊿OAB是等腰三角形又 CA=CB,∴AB⊥OC。 OC是⊙O的半径∴AB是⊙O的切线。连半径,证垂直二、例题讲解小试牛刀如图,已知⊙O的半径为r,...