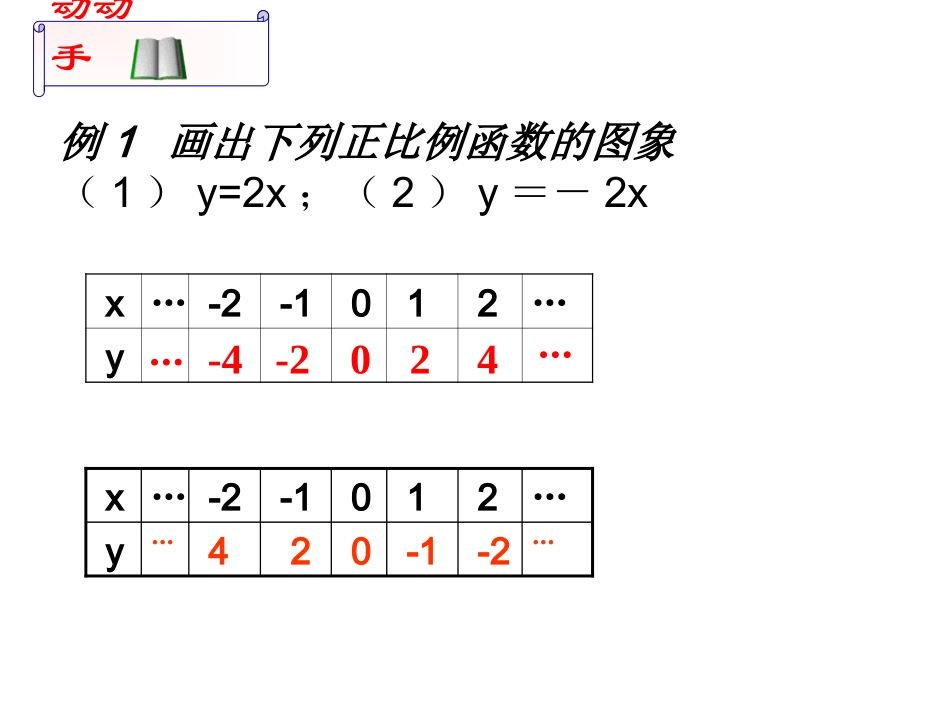
正比例函数图像和性质回顾引入一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.正比例函数的定义:-4-2024x…-2-1012…y……动动手例1画出下列正比例函数的图象(1)y=2x;(2)y=-2x…-2-1024…y…210-1-2…x-5-4-3-2-154321-10-2-3-4-52345y1y=2xxy2x例1画出下列正比例函数的图象(1)y=2x;(2)y=-2x动动手相同点:不同点:函数y=2x的图象经过第象限,从左向右,函数y=-2x的图象经过第象限.从左向右。呈上升状态三、一呈下降状态二、四Yx-4-3-2-10123442-2Yx-4-3-2-10123442-2Y=2xY=-2x两图象都是经过原点的一条直线通过以上学习,画正比例函数图象有无简便的办法?思考xy0xy011y=xy=x21212121正比例函数图象经过点(0,0)和点(1,k)结论xy0xy01k1ky=kx(k>0)y=kx(k<0)练习、在同一平面直角坐标系内,分别画出下列正比例函数的图象:(1)y=x(2)y=x(3)y=-x(4)y=-x2121解(1)正比例函数y=x的图象是经过(0,0),(1,1)的直线21(2)正比例函数y=x的图象是经过(0,0),(2,1)的直线21(4)正比例函数y=-x的图象是经过(0,0),(2,-1)的直线(3)正比例函数y=-x的图象是经过(0,0),(1,-1)的直线y=-xxyo·121xyoy=x·1y=xxyo·121xyoy=-x·1y=xxyo21xyoy=xy=-xxyo21xyoy=-x正比例函数性质:1、图象都经过原点;2、当k>0时,它的图象经过第一、三象限,3、当k<0时,它的图象经过第二、四象限,对于正比例函数y=kx(1)(2)(3)(4)y随x的增大而增大;y随x的增大而减少;小结:1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,我们把正比例函数y=kx的图象叫做直线y=kx;2、正比例函数y=kx的图象的画法;3、正比例函数的性质:1)图象都经过原点;2)当k>0时它的图象经过第一、二象限,y随x的增大而增大,当k<0时它的图象经过第二、四象限,y随x的增大而减少。4、正比例函数y=kx在实际应用中、自变量、函数值受实际条件的制约。例2、滑车以每分15米的速度匀速地从轨道的一端滑向另一端已知轨道的长为7米。(1)求滑车滑行的路程S(米)和滑行时间t(分)之间的关系式和自变量t的取值范围;(2)画出图象;(3)根据图象说明当t增大时,S随着增大还是减少?•解:1)s与t的关系式是s=1.5t∵0≤s≤7∴0≤1.5t≤7314∴0≤t≤3140≤t≤即自变量t的取值范围是由于所以函数的图象以O(0,0)B(,7)为端点的一条线段。3140≤t≤3143)由图象可见,当t增大时,s随着增大xyo123451234675•B2)一般地,s=1.5t的图象是过点(0,0)和(1,1.5)的直线,随堂练习2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是()A.m=1B.m>1C.m<1D.m≥1B1.函数y=-7x的图象在第象限内,经过点(0,)与点(1,),y随x的增大而.二、四0-7减少3.直线y=kx经过点(1,—1/2),那么k=—这条直线在第——象限内,直线上的点的纵坐标随横坐标的增大而——。已知点A(a,1),B(-2,b)在这条直线上,则a=—,b=—。4.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,y1)和B(x2,y2),当x1y2,则k的取值范围是()A.k>2B.k<2C.k=2D.无法确定5.正比例函数y=(3m-1)x的图像经过点A(x1,y1)和B(x2,y2),且该图像经过第二、四象限.(1)求m的取值范围(2)当x1>x2时,比较y1与y2的大小,并说明理由.B如图,三个正比例函数的图像分别对应的解析式是①y=ax②y=bxy=cx,③则a、b、c的大小关系是()A.a>b>cB.c>b>aC.b>a>cD.b>c>a思考xy①②③某函数具有下面的性质:1.它的图象是经过原点的一条直线.2.y随x增大反而减小.请你举出一个满足上述条件的函数,写出解析式.随堂练习如果你是正比例函数代言人,你将怎样介绍它呢例:大家好,我是正比例函数,我有很多优秀的品质,我的解析式是行如,我的图像是我的x与y有很密切的联系