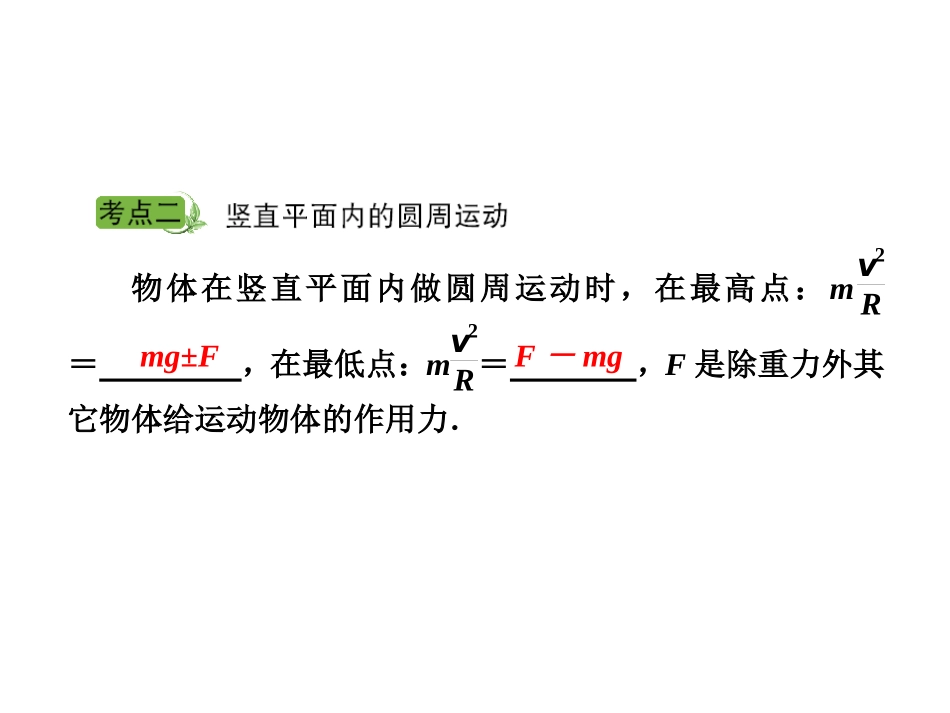
•第四单元圆周运动在实际问题中的应用•由于火车的质量比较大,火车拐弯时所需的向心力就很大.如果铁轨内外侧一样高,则外侧所受的压力很大,容易损坏;实用中使略高于,从而和的合力提供火车拐弯时所需的向心力.外轨重力铁轨支持力内轨物体在竖直平面内做圆周运动时,在最高点:mv2R=,在最低点:mv2R=,F是除重力外其它物体给运动物体的作用力.mg±FF-mg•在平直轨道上匀速行驶的火车,所受合外力为零,在火车转弯时,什么力提供向心力呢?在火车转弯处,让外轨高于内轨,如图1所示,转弯时所需向心力由重力和弹力的合力提供.若轨道水平,转弯时所需向心力应由外轨对车轮的挤压力提供,而这样对车轨会造成损坏.车速大时,容易出事故.设车轨间距为L,两轨高度差为h,车转弯半径为R,质量为M的火车运行时应当有多大的速度?根据三角形边角关系知sinθ=hL,对火车的受力情况分析得tanθ=FMg.因为θ角很小,所以sinθ≈tanθ,故hL=FMg,所以向心力F=hLMg.又因为F=Mv2/R,所以车速v=ghRL.•由于铁轨建成后h、L、R各量是确定的,故火车转弯时的车速应是一个定值,否则将对铁轨有不利影响,如:情况v车>ghRLv车F向不利影响火车挤压外轨火车挤压内轨结果外轨对车轮的弹力补充向心力内轨对车轮的弹力抵消合力•2.静摩擦力作用下的圆周运动•静摩擦力的特点是根据物体运动改变大小,变换方向.有人把静摩擦力的这一特点称为“”适应性.由于静摩擦力这一特点的存在导致在许多问题中出现了临界问题.•处理这类问题的关键是分析出静摩擦力的变化,从而结合其他力分析出向心力的变化,以确定圆周运动的其他物理量的变化范围.•对于物体在竖直面内做的圆周运动是一种典型的变速曲线运动,该类运动常有临界问题,并“”“”“”伴有最大、最小、刚好等词语,常分析——两种模型轻绳模型和轻杆模型,分析比较如下:轻绳模型轻杆模型常见类型轻绳模型轻杆模型过最高点的临界条件由mg=mv2r得v临=gr小球能运动即可,v临=0讨论分析(1)过最高点时v≥gr,FN+mg=mv2r,绳、轨道对球产生弹力FN≥0,方向指向圆心(2)不能过最高点vgr时,FN+mg=mv2r,FN指向圆心并随v的增大而增大•汽车过桥问题•当汽车以相同的速率分别行驶在凸形桥的最高点和凹形桥的最低点时,汽车对桥的压力的区别如下表所示.内容项目凸形桥凹形桥受力分析图内容项目凸形桥凹形桥以a方向为正方向根据牛顿第二定律列方程mg-FN1=mv2rFN1=mg-mv2rFN2-mg=mv2rFN2=mg+mv2r牛顿第三定律FN1′=FN1=mg-mv2rFN2′=FN2=mg+mv2r讨论v增大,FN1′减小;当v增大到gr时,FN1′=0v增大,FN2′增大,只要v≠0,FN1