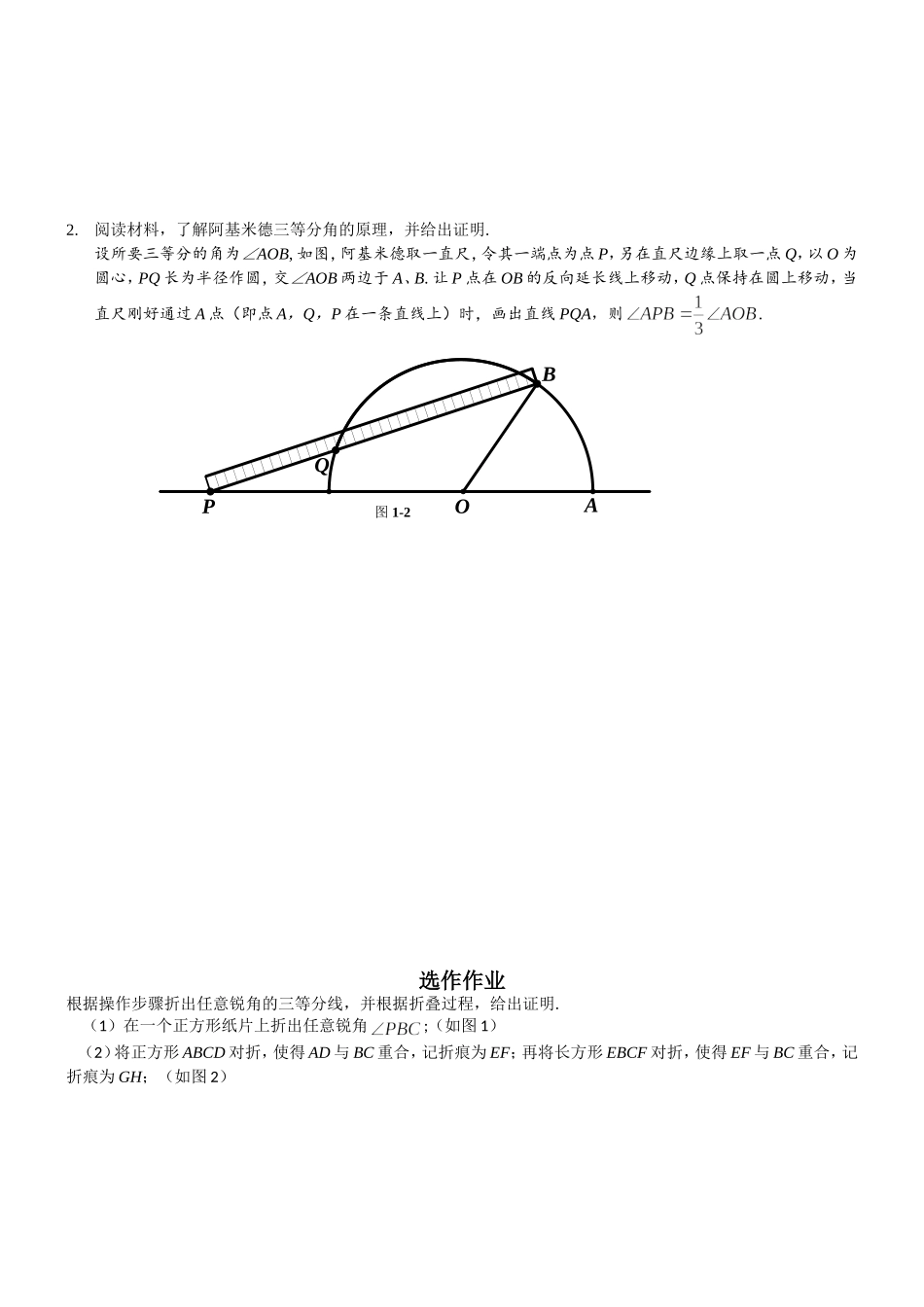
数学活动——三等分角学案问题1:三等分直角CBA问题2:阅读材料:勾尺的直角顶点为P,“宽臂”的宽度=PQ=QR=RS,勾尺的一边为MN,且满足M,N,Q三点共线(所以PQ⊥MN).(1)请根据下面的操作步骤,利用手中的勾尺三等分任意锐角.第一步:画直线DE使DE∥BC,且这两条平行线的距离等于PQ;第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在的BA边上;第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP.BAC(2)证明的三等分线是射线BQ和射线BP.必做作业1.规范书写问题1和2的证明过程.2.阅读材料,了解阿基米德三等分角的原理,并给出证明.设所要三等分的角为∠AOB,如图,阿基米德取一直尺,令其一端点为点P,另在直尺边缘上取一点Q,以O为圆心,PQ长为半径作圆,交∠AOB两边于A、B.让P点在OB的反向延长线上移动,Q点保持在圆上移动,当直尺刚好通过A点(即点A,Q,P在一条直线上)时,画出直线PQA,则.选作作业根据操作步骤折出任意锐角的三等分线,并根据折叠过程,给出证明.(1)在一个正方形纸片上折出任意锐角;(如图1)(2)将正方形ABCD对折,使得AD与BC重合,记折痕为EF;再将长方形EBCF对折,使得EF与BC重合,记折痕为GH;(如图2)图1-2ABOPQCDBAPHGFECDBAP图1图2(3)翻折左下角使B落在GH上,记为B′,且使E落在BP上,记为E′,折痕记为XY,点G折后的点记为G′,折痕XY分别交GH,EF于M,N;(如图3)(4)折BG′和BB′,BB′交XY于Q,则射线BG′,BB′为∠PBC的三等分线.(如图4)G'YXE'HGFECDBAPB'654321QNMG'YXE'GHFEDACBPB'图3图4