12.2.2三角形全等的判定SAS.2.2三角形全等的判定SASVIP免费

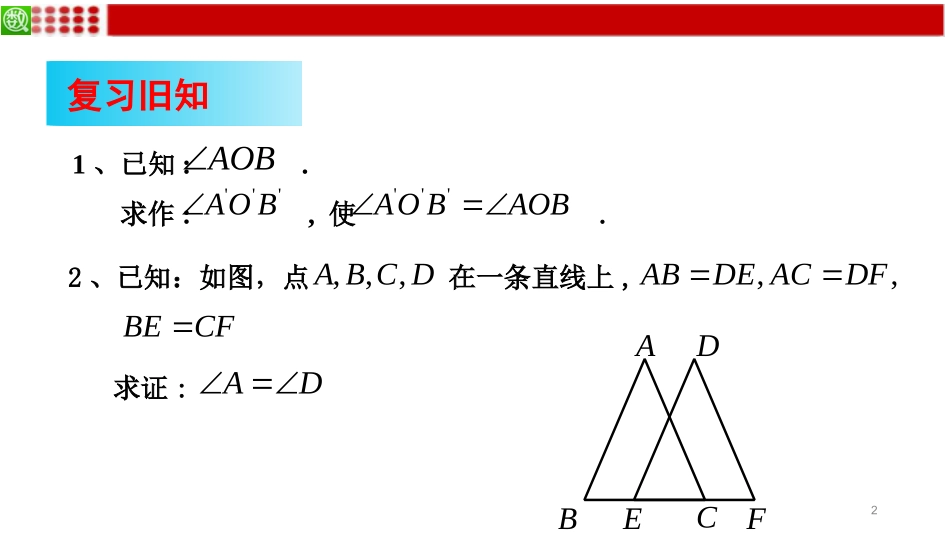
12.2.2三角形全等的判定（2）A′B′C′ABC盘山县坝墙子学校刘莹复习旧知1、已知:.求作:,使.2、已知：如图，点在一条直线上,AOB'''AOB'''AOBAOB,,,ABCD,,ABDEACDFADBECFABCEFD求证:2创设情境如图，有一池塘，要测池塘两端A、B的距离.不能直接测得。只有足够长的量尺，怎么办？DE•CABCD=CA，CE=CB,ACB=DCE∠∠↓△ABCDEC△↓AB=DE?3问题1：已知∠AOB,画一个∠A'O'B'=AOB,∠在射线OAOB上任意选取点C,点D,在射线O'A'截取O'C'=OC,在射线O'B'上截取O'D'=OD.连接△COD和△C'O'D',它们全等么？结论:两边及夹角对应相等的两个三角形全等探究新知AO'A'O'BB••CD'C'D••4三角形全等判定方法2用符号语言表达为：证明：在△ABC和△A′B′C′中∴△ABC≌△A′B′C′（SAS）两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)A′B′C′ABCAC=A′C′∠A=A∠′AB=A′B′5证明三角形全等的步骤：1.写出在哪两个三角形中证明全等.（注意把表示对应顶点的字母写在对应的位置上）；2.按边、角、边的顺序列出三个条件，用大括号合在一起；3.写出结论.注意每步要有推理的依据.6应用新知例2、如图，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长到D,使CD=CA.连结BC并延长到E,使CE=CB.连结DE,那么量出DE的长，就是A、B的距离.为什么？DE•CABCD=CA，CE=CB,ACB=DCE∠∠↓△ABCDEC△↓AB=DE7应用新知DE•CAB证明:在△ABC和△DEC中△ABCDEC(SAS)≌△（已知）（已知）（对顶角相等）（全等三角形对应边相等）∴AB=DEAC=DC∠ACB=DCE∠CB=CE82、怎样找证全等的条件？3、证明线段（或角相等）从已知中找，在图形中看。证明线段（或角）所在的两个三角形全等转化1、怎样用“SAS”去判定三角形全等？在两个三角形中找两边及夹角对应相等三个条件。9辨析理解结论：两边及其一边所对的角相等，两个三角形不一定全等.ACD问题2：如图，将中边旋转，得到。在和中，满足两条边及其中一角对应相等，分别是什么？ABCABDABCABDABCABD追问1:和全等么？追问2:说明了什么？ACABDABC10B基础训练1、使成立的条件是（）ABCADC.,AABADBD.,BABADACBACD.,CBCDCBACDAC.,DABADBACDACADBCD11基础训练2、补充条件，使结论成立：AO=DO(已知)______=________()BO=CO(已知)∴△AOBDOC≌△（）对顶角相等SASABDOC∠AOB∠DOC如图,在△AOB和△DOC中12基础训练3、补充条件，使结论成立：AB=EB(已知)∠ABC=EBD∠______=_______∴△ABCEBD≌△（）SAS如图,在△ABC和△EBD中AEDCBBCBD13综合提高4、已知：如图，AB=AC，AD=AE，∠CAB=DAE∠，求证：△ABD≌ACE.△ACBED证明∵∠CAB=DAE∠，∴∠CAB+EAB=DAE+EAB∠∠∠即∠EAC=∠DAB在△ABD和△ACE中AB=AC（已知）∠DAB=EAC∠（已证）AD=AE（已知）∴△ABD≌ACE△（SAS）145、如图,BC∥AD,BC=AD.求证：AB=DCABCD综合提高证明∵BCAD∥∴∠DAC=BCA(∠两直线平行，同位角相等）在△ADC和△ABC中BC=AD（已知）∠DAC=BCA∠(已证）AC=CA(公共边)∴△ADC≌ABC△(SAS)∴AB=DC(全等三角形对应边相等）15综合提高6、已知：如图，ADBC,AD=BC,AE=CF,AF=5,AE=2,∥求AC的长.∴AE+EF=CF+EF即AF=CE∴∠A=C(∠两直线平行,内错角相等)在△ADF和△CEB中AD=CB（已知）∠A=C∠(已证）AF=CE(已证)∴△AFD≌CEB△(SAS)证明∵AE=CF∵ADBC∥EDAFBC∴CE=AF=5cm∵AE=2cm∴AC=CE+AE=5+2=7cm1、边角边公理：2、边角边公理的应用中所用到的数学方法:证明线段（或角相等）转化同学们：这节课我们学到了什么呢？有两边和它们的夹角对应相等的两个三角形全等.(可以简写成“边角边”或“SAS”）课堂小结证明线段（或角）所在的两个三角形全等17课后作业1、必做题：习题12.2第2、3题。2、选做题：习题12.2第10题。3、预习：教科书第39----41页。谢谢，再见！