1.3.2函数的最大最小值VIP免费

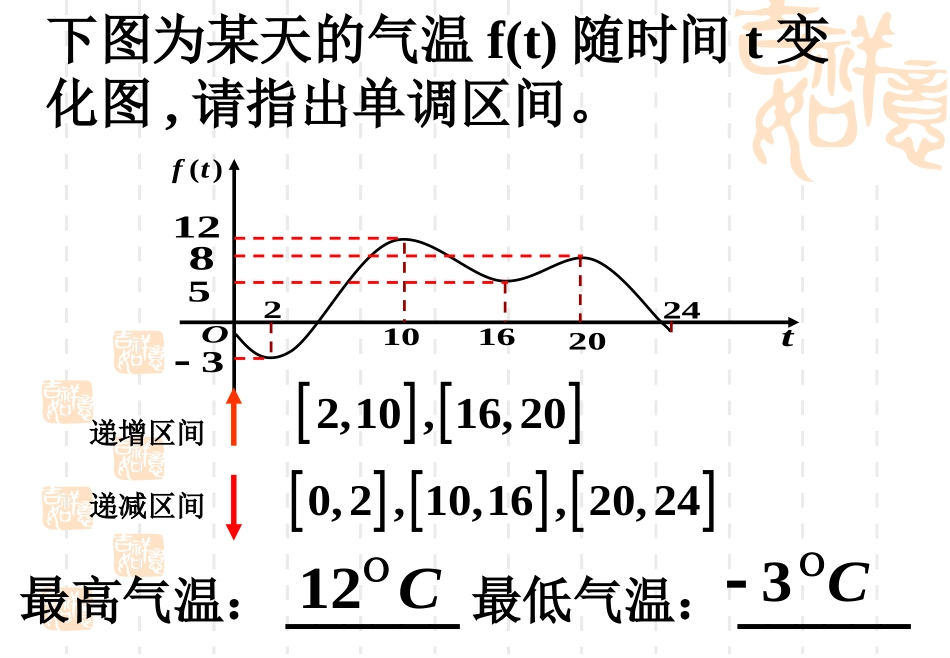
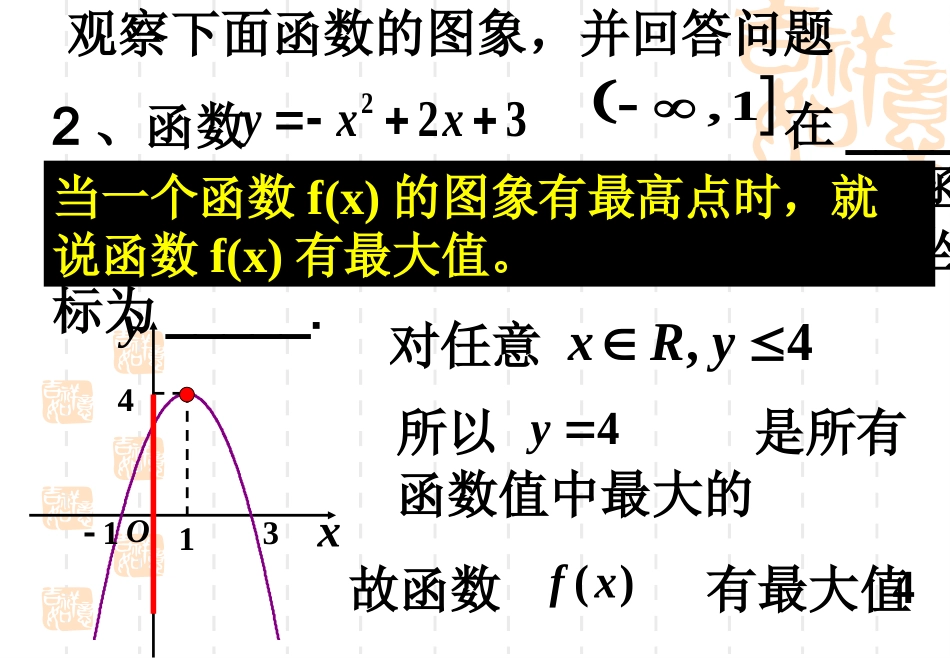
函数的基本性质————最大最小值t()ftO24102016235128下图为某天的气温f(t)随时间t变化图,请指出单调区间。0,2,10,16,20,242,10,16,20最高气温：______最低气温：______12C3C递增区间递减区间xyO13142、函数在_______上为增函数，在________上为减函数;图象有_____(最高（低）)点，坐标为_____.223yxx观察下面函数的图象，并回答问题,4xRy对任意所以是所有函数值中最大的4y故函数有最大值()fx4,11,1,4最高当一个函数f(x)的图象有最高点时，就说函数f(x)有最大值。3、函数在_______上为增函数，在________上为减函数；图象有_____(最高（低）)点，坐标为______.223yxx观察下面函数的图象，并回答问题xyO1314,4xRy对任意所以是所有函数值中最小的4y故函数有最小值()fx4,11,最低1,4当一个函数f(x)的图象有最低点时，就说函数f(x)有最小值。2、当一个函数f(x)的图象有最低点时，就说函数f(x)有最小值。1、当一个函数f(x)的图象有最高点时，就说函数f(x)有最大值。三、最大值的定义：一般地，设函数f(x)的定义域为Ｉ，如果存在实数Ｍ满足：（１）对于任意的那么，我们称M是函数的最大值。你是怎样理解这个定义的？;)(,MxfIx都有00(2),().xIfxM存在使得可以这样理解：函数的最大值是所有函数值中最大的一个，并且是能够取到的。四、最小值的定义：一般地，设函数f(x)的定义域为Ｉ，如果存在实数Ｍ满足：（１）对于任意的;)(,MxfIx都有00(2),().xIfxM存在使得可以这样理解：函数的最小值是所有函数值中最小的一个，并且是能够取到的。下列函数是否存在最大值、最小值？函数在何处取得最大值和最小值,并求出其值。(1)2,()yxxR(2)2,(13)yxx(3)2,(13)yxx没有在x=1时取得最小值2；在x=3时取得最大值6在x=1时取得最小值2；没有最大值2(4)2,yxxxR1(5),yxRx1(6),1,5yxx在x=1时取得最小值-1;没有最大值没有最小值；没有最大值在x=5时取得最小值;在x=1时取得最大值115求函数的最大值.241612()yxxxR解：22416124228yxxx如图，函数在上增函数，在上是减函数。,22,()fxxyO228所以，时2xmax28yhmts2()41612htttxyO例3：“菊花”烟花是最壮观的烟花之一。制造时一般是期望在它达到最高点时爆裂。如果烟花距地面的高度与时间之间的关系为，那么烟花冲出后什么时候是它爆裂的最佳时刻？这时距地面的高度是多少（精确到1m）？解：22()416124228htttt如图，函数在上增函数，在上是减函数。0,22,()ht所以，时2tmax28hthO228由题可知，0t答：烟花冲出后2s是爆裂的最佳时刻，这时距地面的高度为28m。如果函数y=f(x)在区间[a，b]上单调递增，则函数y=f(x)在x=a处有最小值f(a)，在x=b处有最大值f(b)；如果函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增，则函数y=f(x)在x=b处有最小值f(b)。三、利用函数单调性判断函数的最大(小)值的方法：例2:已知函数(1)求证f(x)在区间[2,6]上是单调递减;(2)求函数的最大值和最小值。2,2,61fxxx)1)(1()(2)1)(1()]1()1[(21212)()(121212122121xxxxxxxxxxxfxf由于20,(x1-1)(x2-1)>0,于是)()(,0)()(2121xfxfxfxf即所以，函数是区间[2,6]上的减函数.12xy因此,函数在区间[2,6]上的两个端点上分别取得最大值和最小值，即在点x=2时取最大值，最大值是2，在x=6时取最小值，最小值为0.4.12xy先说明函数在区间上是减函数，复习一下判定函数单调性的基本步骤。利用函数的单调性来求函数的最大值与最小值是一种十分常用的方法，要注意掌握。解：任取x1,x2[2,6]∈，且x1＜x2练习：求函数的最大值和最小值。2(2)23,1,2yxxx2(3)23,2,1yxxx2(1)23,yxxxR1x时，min2y1x时，min2;y2x时，max3y1x时，...