26.1.2反比例函数的图象与性质(一).1.2反比例函数VIP免费

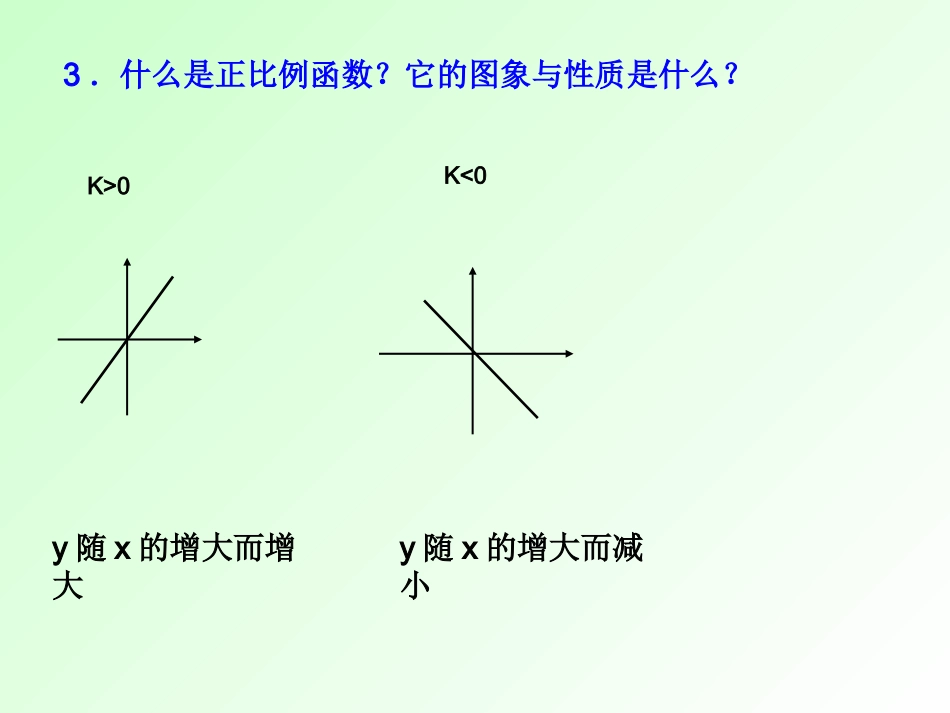
第1课时26.1.2反比例函数的图象与性质1．什么是反比例函数？2．反比例函数的定义中需要注意什么？（1）k是非零常数.（2）xy=k．一般地，形如y=(k是常数,k≠0)的函数叫做反比例函数．kx—K>03．什么是正比例函数？它的图象与性质是什么？y随x的增大而增大y随x的增大而减小K<0x画出反比例函数和的函数图象。y=x6y=x6画函数图象列表描点连线y=x6y=x6操作一：123456-1-3-2-4-5-61234-1-2-3-40-6-556yxxy=x6y=x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……........123456-1-3-2-4-51234-1-2-3-40-6-556y=x6y=-x6-6xy请大家仔细观察反比例函数和的函数图象，找找看，他们有什么共同的特征？xy6xy6操作二：比一比：分别画出函数的图象。xyxy3,3找一找：１、这几个函数图象有什么共同点？２、函数图象分别位于哪几个象限？３、y随x的变化有怎样的变化？根据大家所画出的函数图象，从以下几个方面出发，你能发现反比例函数的图象及性质有哪些？)0(kxky123456-1-3-2-4-51234-1-2-3-40-6-556y=x6y=-x6xy3xy3Xy１、这几个函数图象（k>0，k<0）有什么共同点？２、函数图象分别位于哪几个象限？（分k>0，k<0两种情况）３、y随的x变化有怎样的变化？提示：探索性质由两支曲线组成的.因此称它的图象为双曲线;当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;当k>0时,在每一象限内,y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大.反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴⑴反比例函数的图象是轴对称图形.直线y=x和y=-x都是它的对称轴；⑵反比例函数与的图象关于x轴对称,也关于y轴对称。（3）反比例函数的图象是中心对称图形.对称中心是原点.反比例函数的图象和性质形状位置增减性图象的发展趋势对称性kyxkyxA：xyoB：xyoD：xyoC：xyo1、反比例函数y=-的图象大致是（）x5D函数y=kx-k与在同一条直角坐标系中的图象可能是:xyoxyoxyoxyo(A)(B)(C)(D)0kykx练一练1D函数的图象在第________象限,在每一象限内，y随x的增大而_________.函数的图象在第________象限,在每一象限内，y随x的增大而_________.函数,当x>0时,图象在第____象限,y随x的增大而_________.一、三二、四一减小增大减小yx30yx20yx练一练22练一练33已知反比例函数(1)若函数的图象位于第一三象限，则k_____________;(2)若在每一象限内，y随x增大而增大，则k_____________.4kyx<4>4已知反比例函数xy2（1）点(-2,y1),(-1,y2)在该函数的图象上，y1y2（2）点(2,y1),(1,y2)在该函数的图象上，y1y2（3）点(-2,y1),(1,y2)在该函数的图象上，y1y2（4）点(-2,y1),(1,y2),(3,y3)在该函数的图象上y1,y2,y3的大小关系如何？练一练44•已知反比例函数上有两点A（x1,y1),B(X2,y2)，且x1＞x2＞0时，y1＜y2.则k取值范围是kyx练一练44函数正比例函数反比例函数解析式图象形状K>0K<0位置增减性位置增减性y=kx(k≠0的常数)(k≠0的常数)y=xk直线双曲线一三象限y随x的增大而增大一三象限二四象限y随x的增大而减小在每个象限内，y随x的增大而增大比较正比例函数和反比例函数的区别二四象限在每个象限内，y随x的增大而减小1.通过本节课的学习，你有什么收获？还有什么困惑吗？2.你对自己本节课的表现满意吗？为什么？数缺形时少直觉，形少数时难入微．