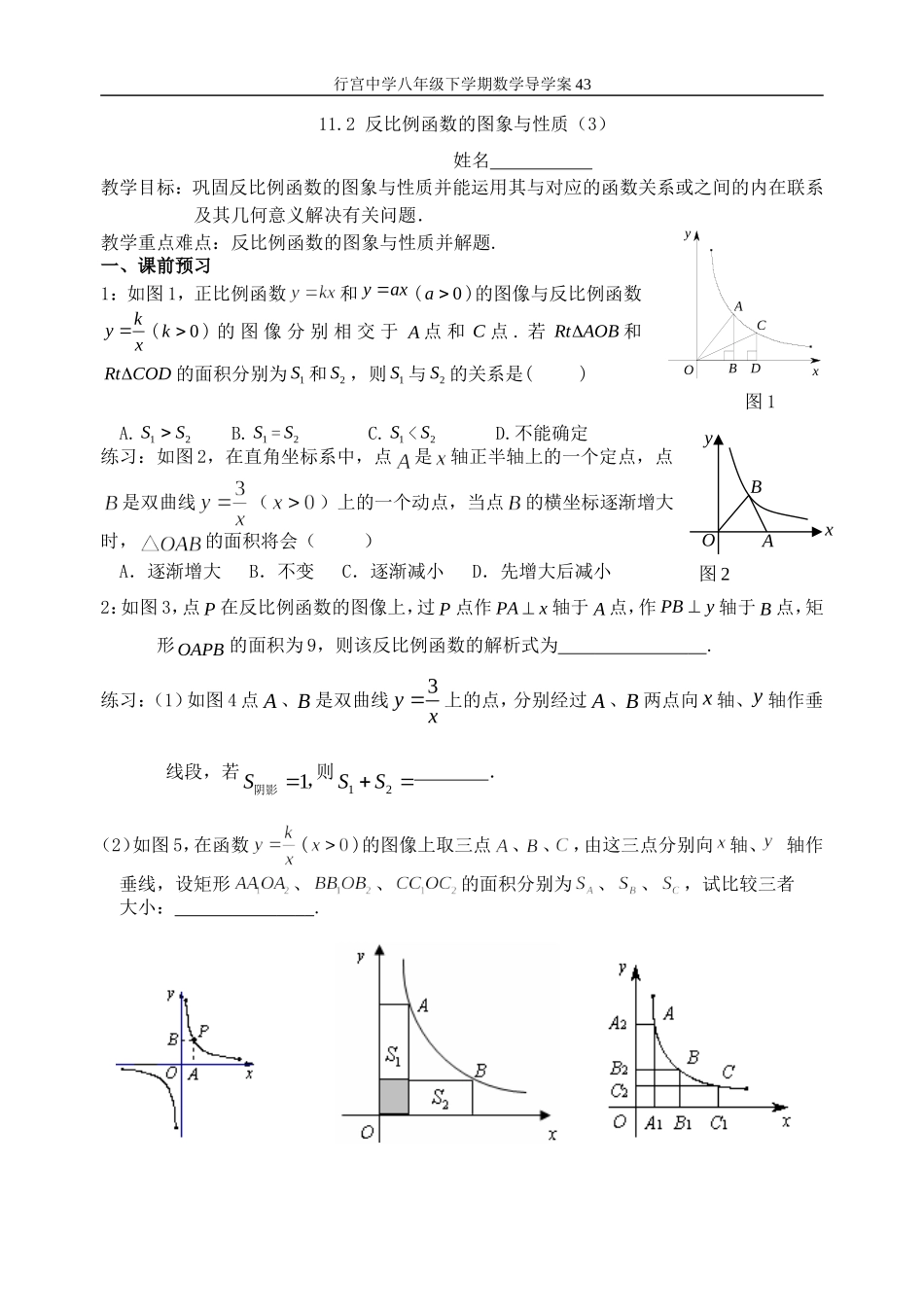
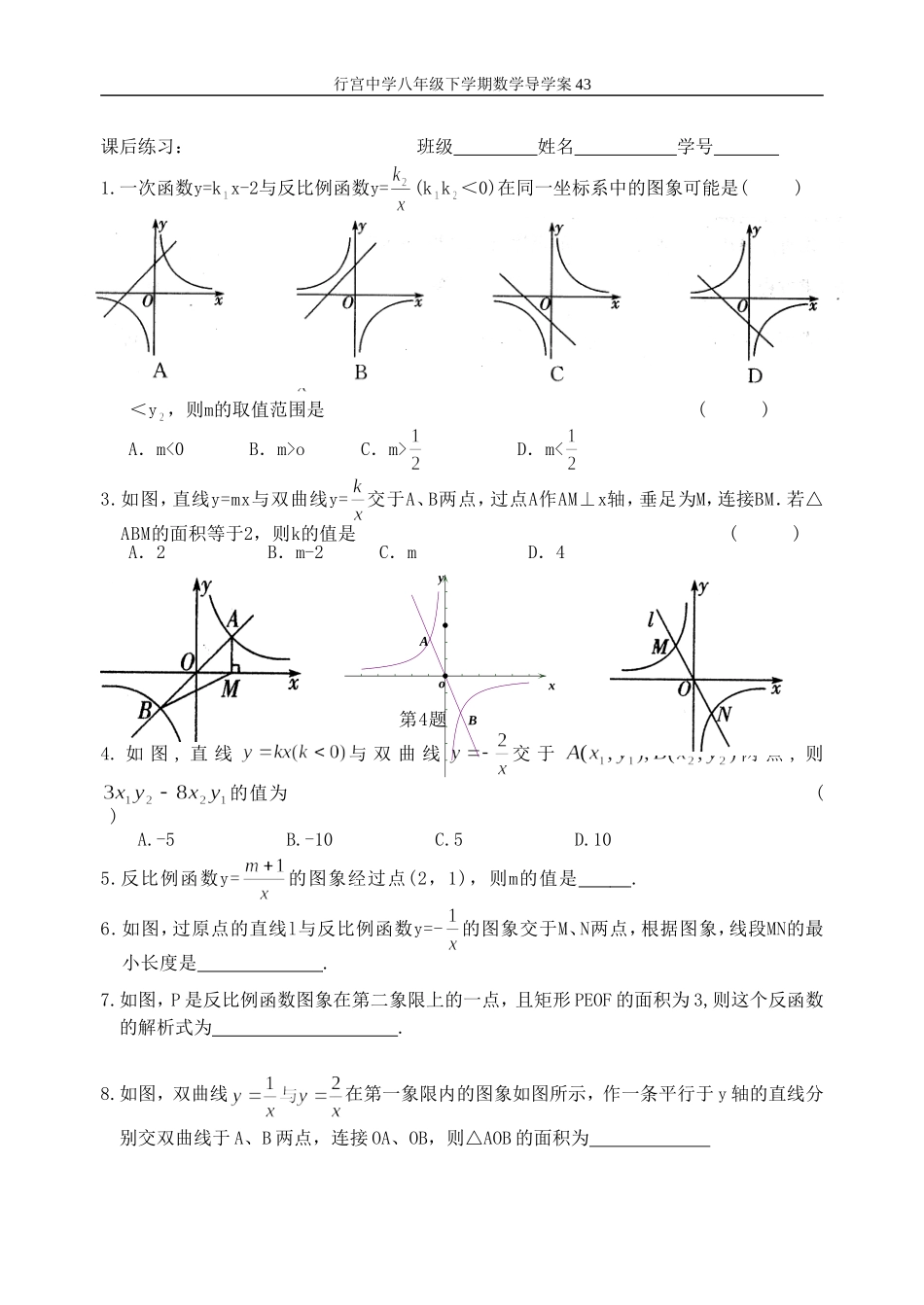
xyOAB图2行宫中学八年级下学期数学导学案4311.2反比例函数的图象与性质(3)姓名教学目标:巩固反比例函数的图象与性质并能运用其与对应的函数关系或之间的内在联系及其几何意义解决有关问题.教学重点难点:反比例函数的图象与性质并解题.一、课前预习1:如图1,正比例函数和yax(0a)的图像与反比例函数kyx(0k)的图像分别相交于A点和C点.若RtAOB和RtCOD的面积分别为1S和2S,则1S与2S的关系是()图1A.12SSB.1S=2SC.1S<2SD.不能确定练习:如图2,在直角坐标系中,点是轴正半轴上的一个定点,点是双曲线()上的一个动点,当点的横坐标逐渐增大时,的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小2:如图3,点P在反比例函数的图像上,过P点作PAx轴于A点,作PBy轴于B点,矩形OAPB的面积为9,则该反比例函数的解析式为.练习:(1)如图4点A、B是双曲线3yx上的点,分别经过A、B两点向x轴、y轴作垂线段,若1S阴影,则12SS.(2)如图5,在函数()的图像上取三点、、,由这三点分别向轴、轴作垂线,设矩形、、的面积分别为、、,试比较三者大小:.ODCBAxy行宫中学八年级下学期数学导学案43图3图4图5(3)如图,在反比例函数2yx(0x)的图象上,有点1P,2P,3P,4P它们的横坐标依次为1,2,3,4.分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S,2S,3S,求123SSS.3:如图,已知反比例函数kyx的图象与一次函数yaxb的图象交于2Mm,和两点.(1)求这两个函数的解析式;(2)求MON的面积;(3)请判断点是否在这个反比例函数的图象上,并说明理由.练习:1.如图,已知A(4,n),B(2,4)是一次函数ykxb的图象和反比例函数myx的图象的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线AB与x轴的交点C的坐标及AOB△的面积;(3)求方程0mkxbx的解(请直接写出答案);(4)求不等式0mkxbx的解集(请直接写出答案).2.如图,在直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数的图象交于A(-2,1)、B(1,n)两点.(1)求上述反比例函数和一次函数的表达式;(2)连结OA、OB求△AOB的面积.S3S2S11234y=2xP4P3P2xyOP1DNMCBAOyxOCBAyx行宫中学八年级下学期数学导学案43课后练习:班级姓名学号1.一次函数y=kx-2与反比例函数y=(kk<0)在同一坐标系中的图象可能是()2.已知反比例函数y=的图象上有A(x,y)、B(x,y)两点,当x<0oC.m>D.m<3.如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM.若△ABM的面积等于2,则k的值是()A.2B.m-2C.mD.4第3题第4题第6题4.如图,直线与双曲线交于两点,则的值为()A.-5B.-10C.5D.105.反比例函数y=的图象经过点(2,1),则m的值是.6.如图,过原点的直线l与反比例函数y=-的图象交于M、N两点,根据图象,线段MN的最小长度是.7.如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为3,则这个反函数的解析式为.8.如图,双曲线在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为xyBAo行宫中学八年级下学期数学导学案439.函数y1=x(x≥0),y2=(x>0)的图象如图所示,下列结论:①两函数图象的交点坐标为A(2,2);②当x>2时,y2>y1;③直线x=1分别与两函数图象相交于B、C两点,则线段BC的长为3;④当x逐渐增大时,y1的值随x的增大而增大,y2的值随x的增大减少.其中正确的是.第7题第8题第9题10.如图,直线y=kx+b与反比例函数y=(x<0)的图象相交于A、B两点,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为一4.(1)试确定反比例函数的关系式.(2)求△AOC的面积.思维拓展:如图,Rt△AOB顶点A是一次函数的图象与反比例函数的图象在第二象限内的交点,且S△AOB=1.(1)求m的值;(2)求A点坐标.yy1=xy2=x