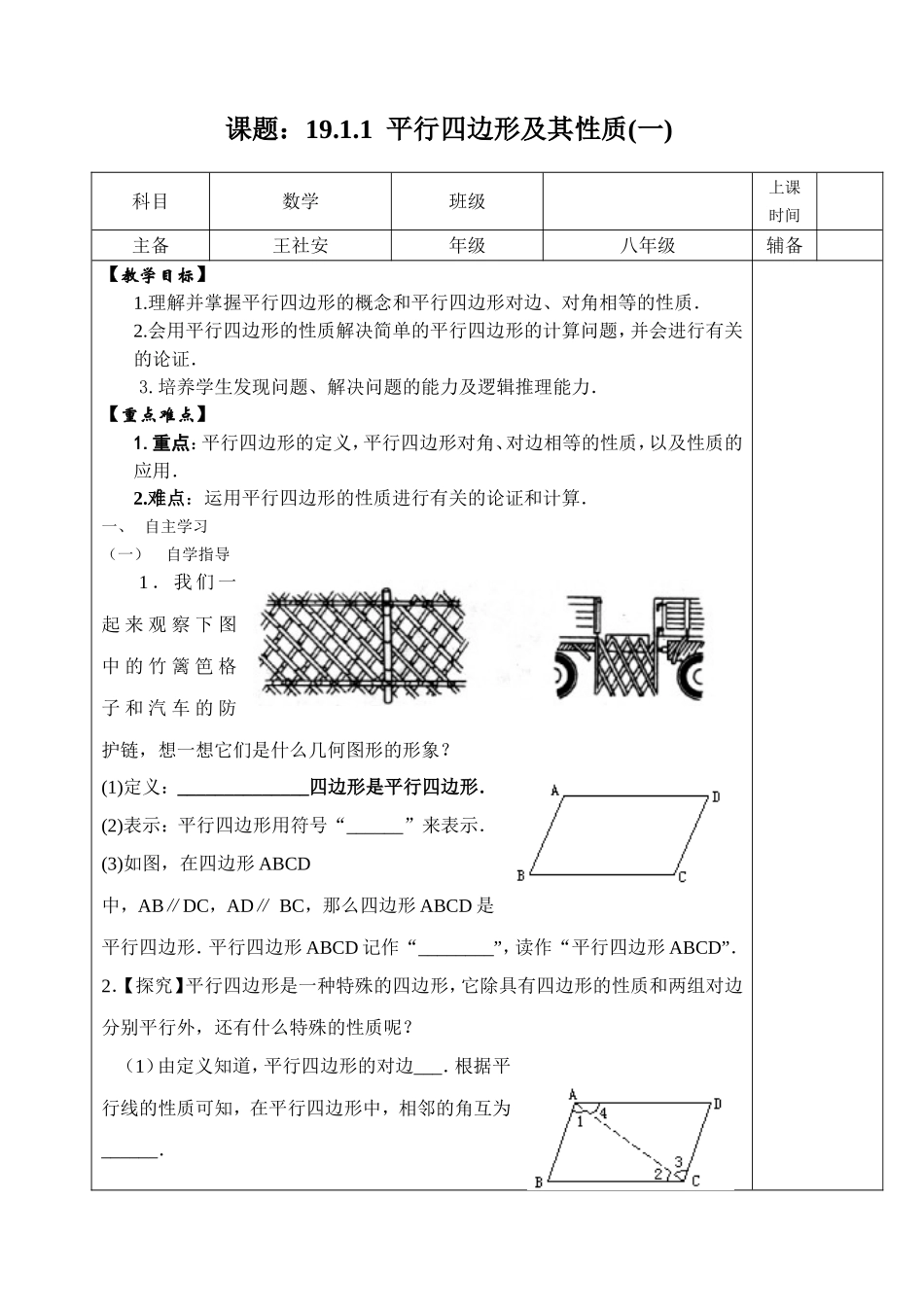
课题:19.1.1平行四边形及其性质(一)科目数学班级上课时间主备王社安年级八年级辅备【教学目标】1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.3.培养学生发现问题、解决问题的能力及逻辑推理能力.【重点难点】1.重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.2.难点:运用平行四边形的性质进行有关的论证和计算.一、自主学习(一)自学指导1.我们一起来观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?(1)定义:______________四边形是平行四边形.(2)表示:平行四边形用符号“______”来表示.(3)如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“________”,读作“平行四边形ABCD”.2.【探究】平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?(1)由定义知道,平行四边形的对边___.根据平行线的性质可知,在平行四边形中,相邻的角互为______.(2)已知:如图ABCD,求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD.(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.)证明:连接AC,∵AB∥CD,AD∥BC,∴∠1=∠3,∠2=∠4.又AC=CA,∴△ABC≌△CDA(_____).∴AB=CD,CB=AD,∠B=∠D.又∠1+∠4=___________,∴∠BAD=____________.由此得到:平行四边形性质1平行四边形的对边____________.平行四边形性质2平行四边形的对角_____________.(二)预习检测例1如图所示,小明用一根36米长的绳子圈成了一个平行四边形的场地,其中一条边AB长为8米,其他三条边各长多少?解:例2、如图ABCD中∠B=∠A,试求∠A、∠B、∠C、∠D的度数.解:二、交流展示交流对本节课预习之后的各自的收获是什么?有什么问题不明白。三、拓展应用①如图ABCD的周长为30cm,且AB:BC=1:2,试求AB、BC、CD、DA的长.②已知平行四边形两对角之和为120°,试求该平行四边形的四个内角分别为多少度DCBADCBADCBA四、反馈达标1.填空:(1)在ABCD中,∠A=,则∠B=度,∠C=度,∠D=度.(2)如果ABCD中,∠A—∠B=24°,则∠A=度,∠B=度,∠C=度,∠D=度.(3)如果ABCD的周长为28cm,且AB:BC=2∶5,那么AB=cm,BC=cm,CD=cm,AD=cm.2.(选择)在下列图形的性质中,平行四边形不一定具有的是().(A)对角相等(B)对角互补(C)邻角互补(D)内角和是3.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有().(A)4个(B)5个(C)8个(D)9个4.如图4.3-9,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.5.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.反思: