正余弦函数图象梁迎花VIP免费

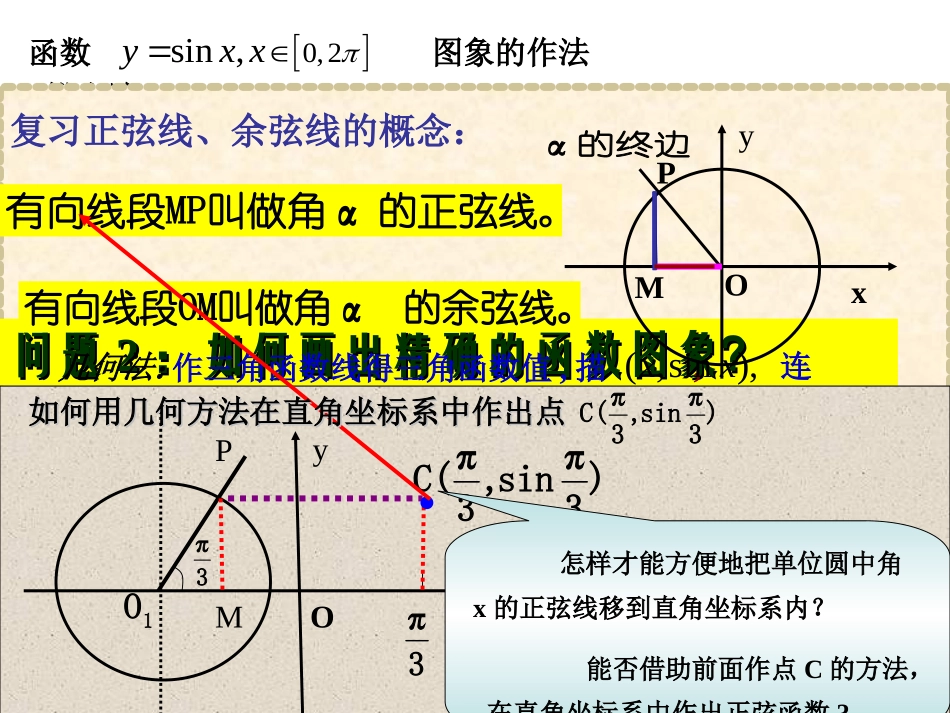
问题问题11：观察简谐振动，注意它的图形特点：观察简谐振动，注意它的图形特点正弦函数、余弦函数的图象第一课时函数0,2sin,yxx图象的作法---223xy0211---描点法:查三角函数表得三角函数值,描点连线.(,sin),xx描点(,0.8660)3,sin0.866033xy如：查表利用三角函数线作三角函数图象？正弦函数图象问题问题22：如何画出精确的函数图象？：如何画出精确的函数图象？复习正弦线、余弦线的概念：PMOxyα的终边的正弦线。有向线段MP叫做角α的余弦线。有向线段OM叫做角α几何法：作三角函数线得三角函数值,描点,连线.(,sin),xxOP1O3πMxy3π32ππ)3πsin,3πC(.如何用几何方法在直角坐标系中作出点如何用几何方法在直角坐标系中作出点)3πsin,3πC(怎样才能方便地把单位圆中角x的正弦线移到直角坐标系内？能否借助前面作点C的方法，在直角坐标系中作出正弦函数?1-1022322656723352yx●●●332346116633265●●●●●●●673435611●●●sin([0,2])yxx[0,2π]的图象xsinx,用几何方法作y1描图：用光滑曲线将这些正弦线的终点连结起来问题问题33：为什么要从单位圆与：为什么要从单位圆与xx轴相交点轴相交点AA开始，将单位圆开始，将单位圆1212等份？等份？x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322探究探究11：如何做出：如何做出y=siny=sinx((xR)∈R)∈的函数图象？的函数图象？因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2即：sin(x+2k)=sinx,kZxy1-1cossin()2yxx2余弦函数的图像可以通过正弦曲线向左平移各单位长度而得到．探究探究22：如何做出：如何做出y=cosy=cosx((xR)∈R)∈的函数图象？的函数图象？余弦曲线2oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法”。问题问题44：做正弦函数时应当抓住哪些关键点：做正弦函数时应当抓住哪些关键点？？-oxy---11--13232656734233561126cos[0,2]yxx在函数的图象上，起关键作用的点有：cos,[0,2]yxx最高点：最低点：与x轴的交点：(0,1)3(,0)2(2,1)(,1)(,0)2简图作法(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)问题问题55：做余弦函数时应当抓住哪些关键点：做余弦函数时应当抓住哪些关键点？？例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]探究3:从另一个角度从另一个角度说出:函数y=1+sinx和y=sinx的图象有何联系？y=1+sinx由y=sinx向上平移1个单位得到。例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]探究4:从另一个角度从另一个角度说出:函数y=-cosx和y=cosx的图象有何联系？这两个图像关于x轴对称。xsinx2230210-101练习：在同一坐标系内，用五点法分别画出函数y=sinx，x[0,2]和y=cosx，x[,]的简图：223o1yx22322-12y=sinx，x[0,2]y=cosx，x[,]223向左平移个单位长度2xcosx100-1022302总结归纳yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]（1）利用正弦线画出正弦函数的图象。（2）利用正弦函数的图象和诱导公式画出余弦函数的图象。（3“”）用五点作图法画正弦函数、余弦函数的简图。(4)注意与诱导公式、三角函数线等知识的联系作业课本第46页习题第1题x3x2π23ππ2π06π29π3π23π03sinx010-100xy6π29π3π23π1-1.....2π23ππ2π03π2x310π37π34π3π32π-x02-020y310π37π34π3πO32π-XY.....-22)3π2x2sin(y用五点法分别画出函数的简图