高中数学导数及其应用教案函数的极值与导数新课标人教A版VIP免费

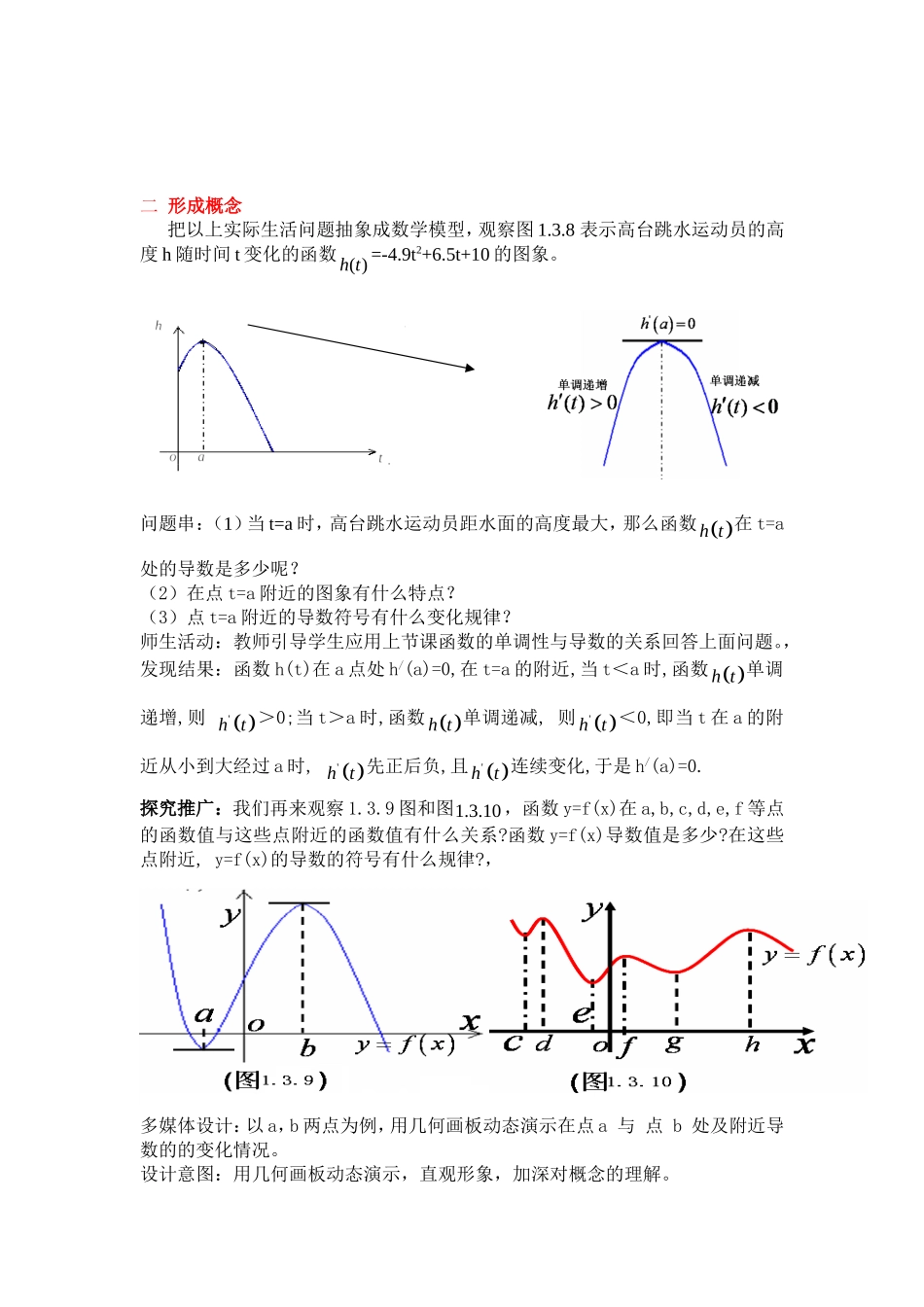
1.3.2函数的极值与导数教学分析：本节内容是导数研究函数性质的继续深入，在教材中起到了承上启下的作用是本章的重要知识点，也是导数应用的关键知识点。通过对函数极值的判定，使学生加深对函数单调性与其导数关系的理解；掌握了函数极值的判别法，为学生下一节学习函数最大、最小值与导数铺平了道路。三维目标1知识与技能〈1〉结合函数图象，了解可导函数在某点取得极值的必要条件和充分条件〈2〉理解函数极值的概念，会用导数求函数的极大值与极小值2过程与方法结合实例，借助函数图形直观感知，探索函数的极值与导数的关系。3情感，态度与价值观感受导数在研究函数性质中一般性和有效性，通过学习让学生体会极值是函数的局部性质，增强学生数形结合的思维意识。重点难点：教学重点：正确理解函数极值的概念，学会用导数判别函数极值的方法。教学难点：函数在某点取得极值的必要条件和充分条件。教学手段：多媒体辅助教学教学流程：二、教学基本流程教学过程一情景导入大家观看过高台跳水吗？是否被运动员在高空用身躯画出的完美曲线的而折服？请同学们分析一下运动员从起跳到落水的运动状态的变化。设计意图：数学来源于生活，激发学生兴趣，渗透德育教育。形成概念，深化概念：关系应用举例：通过例题和练习，学会求函数极值情景导入探究发现归纳小结，设计作业二形成概念把以上实际生活问题抽象成数学模型，观察图1.3.8表示高台跳水运动员的高度h随时间t变化的函数()ht=-4.9t2+6.5t+10的图象。问题串：（1）当t=a时，高台跳水运动员距水面的高度最大，那么函数ht在t=a处的导数是多少呢？（2）在点t=a附近的图象有什么特点？（3）点t=a附近的导数符号有什么变化规律？师生活动：教师引导学生应用上节课函数的单调性与导数的关系回答上面问题。，发现结果：函数h(t)在a点处h/(a)=0,在t=a的附近,当t＜a时,函数ht单调递增,则'ht＞0;当t＞a时,函数ht单调递减,则'ht＜0,即当t在a的附近从小到大经过a时,'ht先正后负,且'ht连续变化,于是h/(a)=0.探究推广：我们再来观察1.3.9图和图10.3.1，函数y=f(x)在a,b,c,d,e,f等点的函数值与这些点附近的函数值有什么关系?函数y=f(x)导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律?，多媒体设计：以a，b两点为例，用几何画板动态演示在点a与点b处及附近导数的的变化情况。设计意图：用几何画板动态演示，直观形象，加深对概念的理解。师生活动：让学生先试着归纳总结，教师再补充，培养学生归纳概括能力。以a,b两点为例，我们可以发现，函数xfy在点ax的函数值af比它在点ax附近其他点的函数值都小，af'=0；而且在点ax附近的左侧xf'＜0，右侧xf'＞0。类似的，函数xfy在点bx的函数值bf比它在点bx附近其他点的函数值都大，bf'=0；而且在点bx附近的左侧xf'＞0，右侧xf'＜0。我们把点a叫做函数y=f(x)的极小值点，f(a)叫做函数y=f(x)的极小值；点b叫做函数y=f(x)的极大值点，f(a)叫做函数y=f(x)的极大值。极大值点与极小值点称为极值点,极大值与极小值称为极值.三深化概念问题1：通过几个条件可以确定函数在某点处有极值？(即函数在某点处取得极值的充分条件是什么?)①函数f(x)在0x的导数值00'xf②在0x附近的左右两侧xf'的符号为异号问题2：极大值一定比极小值大吗？让学生观察图10.3.1,可得，极值反映的是函数的局部性质。课本练习29P1下图是导函数'fx的图象，试找出函数xf的极值点，并说出哪些是极大值点,哪些是极小值点.四应用举例例1求函数31443fxxx的极值师生活动：学生思考交流，教师引导学生从极值的定义出发考虑解决问题的思路，教师板演解题过程，起到示范作用。解: 31443fxxx∴'fx=x2-4=(x-2)(x+2)令'fx=0,解得x=2,或x=-2.下面分两种情况讨论:(1)当'fx＞0,即x＞2,或x＜-2时;（2）当'fx＜0,即-2＜x＜2时.当x变化时,'fx,f(x)的变化情况如下表:x(-∞,-2)-2(-2,2)2(2,+∞)'fx+0_0+f(x)单调递增283单调递减43单调递增因此,当x=-2时,f(x)有极大值,且极大值为f(-2)=283;当x=2时,f...