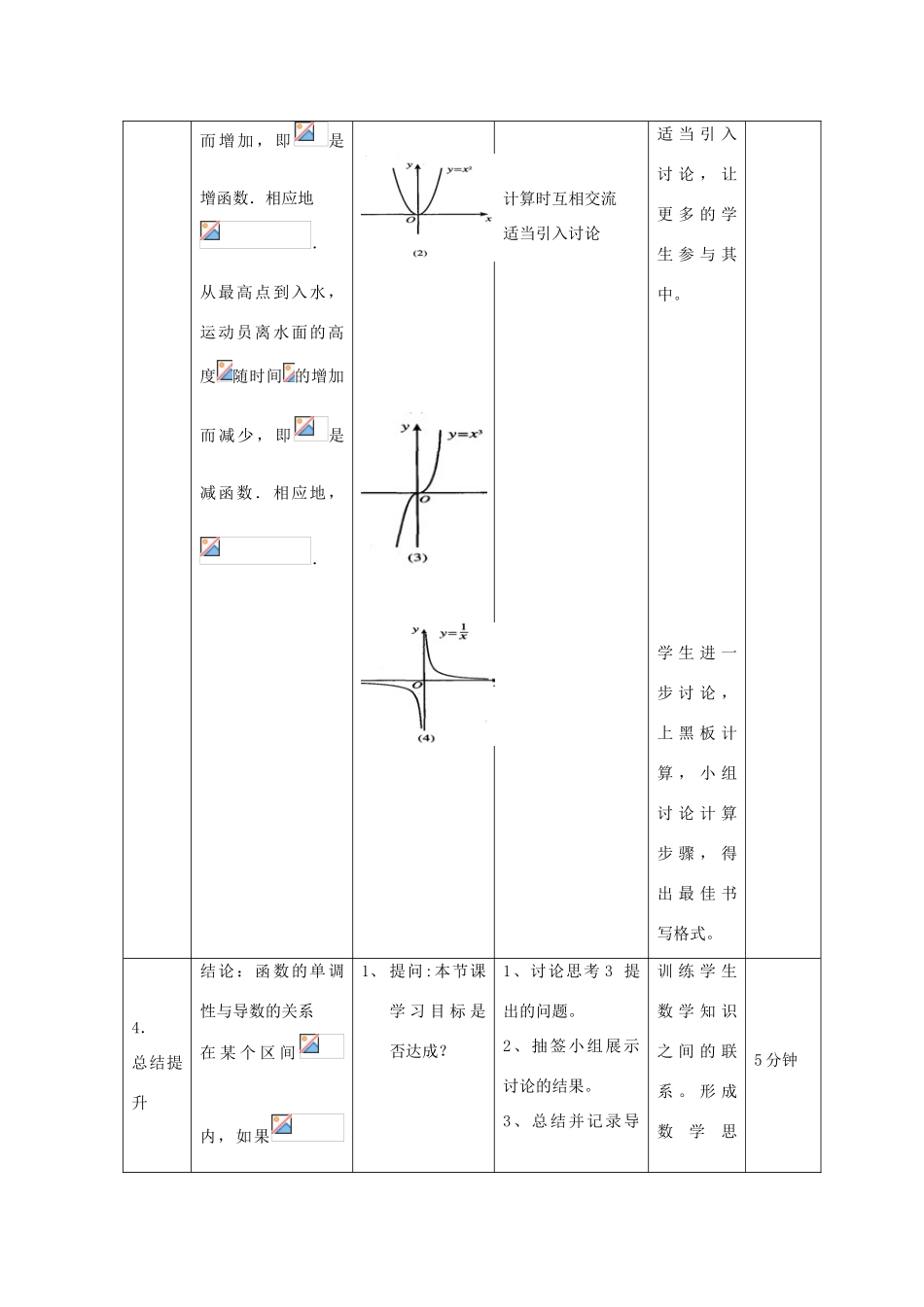
利用导数判断函数单调性课题利用导数判断函数单调性一课时第一课时课型新授教学重点学生会利用导数研究函数的单调性。会求不超过三次的多项函数的单调区间依据:2017年高考大纲分析:理解导数。教学难点会求不超过三次的多项式的函数单调区间。依据:学生刚接触到变化的概念与图像的关系自主学习目标1.学生能认识到可导函数的单调性与导数的关系;2.学生能利用导数研究函数单调性。;3.学生会求函数的单调区间。4、学生通过求导,计算函数单调区间。5、学生能进一步发展数学运算能力理由:能研究函数单调区间,会求单调区间,教具多媒体课件、教材,教辅教学环节教学内容教师行为学生行为设计意图时间1.课前3分钟1、教辅第88页《预习自测》1-52、目标解读检查,评价总结小考结果。1.小考:《预习测评》1-52.提出自主学习困惑.明确本节课学习目标,准备学习。3分钟2.承接结果一.创设情景函数是客观描述世界变化规律的重要数学模型,研究函数时,了解函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的.通过研究函数的这1.问题:图1.3-1(1),它表示跳水运动中高度随时间变化的函数的图像,图3.3-注:在本环节中不急于向学生交待导数的定义。而是先设计一个实13分钟些性质,我们可以对数量的变化规律有一个基本的了解.下面,我们运用导数研究函数的性质,从中体会导数在研究函数中的作用.1(2)表示高台跳水运动员的速度随时间变化的函数的图像.例,一来是为了给学生一个创造观察的机会,让学生体会导数的物理引入;变化以及变化率的公式的计算和表达3.做、议讲、评运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?通过观察图像,我们可以发现:运动员从起点到最高点,离水面的高度随时间的增加2.函数的单调性与导数的关系观察下面函数的图像,探讨函数的单调性与其导数正负的关系.学生在笔记本上计算学生在黑板上计算通过具体实例做题,加深对变化率公式的记忆和计算。印象深刻。计算时,10分钟而增加,即是增函数.相应地.从最高点到入水,运动员离水面的高度随时间的增加而减少,即是减函数.相应地,.计算时互相交流适当引入讨论适当引入讨论,让更多的学生参与其中。学生进一步讨论,上黑板计算,小组讨论计算步骤,得出最佳书写格式。4.总结提升结论:函数的单调性与导数的关系在某个区间内,如果1、提问:本节课学习目标是否达成?1、讨论思考3提出的问题。2、抽签小组展示讨论的结果。3、总结并记录导训练学生数学知识之间的联系。形成数学思5分钟,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.说明:(1)特别的,如果,那么函数在这个区间内是常函数.2、引导学生总结图形的变化关系。3、如图1.3-3,导数表示函数在点处的切线的斜率.4、数定义和意义维。5.目标检测随堂测试小卷1、巡视学生作答情况。2、公布答案。3、评价学生作答结果。1、小考卷上作答。2、同桌互批。3、独立订正答案。检查学生对本课所学知识的掌握情况。5分钟6布置下节课自主学习1、阅读教材,完成课后练习A组(同桌检查并签字),思考练习B组题(要求有痕迹)。2、熟记平均变化率的导数定义和几何意义(组长检查)。让学生明确下节课所学,有的放矢进行自4分钟任务3、完成预习习题卷(上课抽查)主学习。7板书设计导数与函数单调性例题展示:例1:1、单调性定义:例2:2、单调性认识:3、习题:8课后反思导数的基础认识,导数的应用,结合图像认识导数。