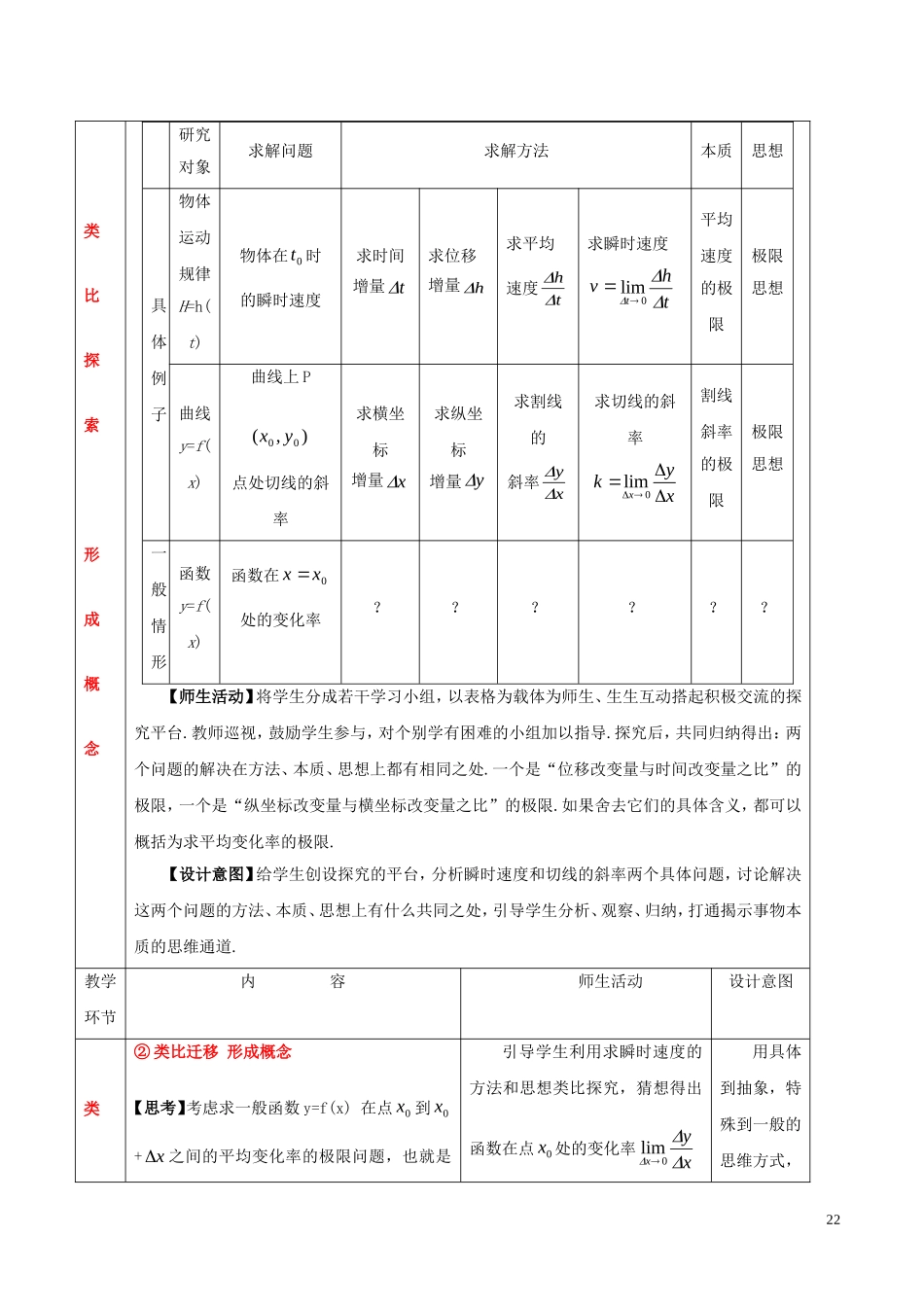
1§1.1.2导数的概念教学目标:1.了解瞬时速度、瞬时变化率的概念;2.理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵;3.会求函数在某点的导数。教学重点:瞬时速度、瞬时变化率的概念、导数的概念;教学难点:导数的概念.(一)、情景引入,激发兴趣【教师引入】:“生活中有一些现象值得我们去研究,比如,子弹离开枪管那一瞬间的速度,奥运会上百米赛跑运动员冲向终点那一时刻的速度。科学上对瞬时速度的研究也是非常有必要的,比如在天宫一号与神州八号的成功对接,最关键的就是它们每个瞬间的速度都相等。(二)、探究新知,揭示概念教学环节内容师生活动设计意图复习引入提出问题【回顾1】当运动员从10米高台跳水时,从腾空到进入水面的过程中,不同时刻的速度是不同的.假设t秒后运动员相对地面的高度为:105.69.4)(2tttH,问在2秒时运动员的瞬时速度为多少?【回顾2】已知曲线C是函数105.69.4)(2xxxf的图象,求曲线上点P),(00yx处的切线斜率.【思考】对瞬时速度和和切线的斜率两个具体问题,解决方法上有什么共同之处?学生相互交流探讨瞬时速度和和切线的斜率两个具体问题,解决方法上有什么共同之处.针对新概念创设相应的学生熟悉的问题情景,让学生从概念的现实原型,体验、感受直观背景和概念间的关系,为学生主动建构新知提供自然的生长点.①归纳共性揭示本质12类比探索形成概念研究对象求解问题求解方法本质思想具体例子物体运动规律H=h(t)物体在0t时的瞬时速度求时间增量t求位移增量h求平均速度th求瞬时速度vtht0lim平均速度的极限极限思想曲线y=f(x)曲线上P),(00yx点处切线的斜率求横坐标增量x求纵坐标增量y求割线的斜率xy求切线的斜率0limxykx割线斜率的极限极限思想一般情形函数y=f(x)函数在0xx处的变化率??????【师生活动】将学生分成若干学习小组,以表格为载体为师生、生生互动搭起积极交流的探究平台.教师巡视,鼓励学生参与,对个别学有困难的小组加以指导.探究后,共同归纳得出:两个问题的解决在方法、本质、思想上都有相同之处.一个是“位移改变量与时间改变量之比”的极限,一个是“纵坐标改变量与横坐标改变量之比”的极限.如果舍去它们的具体含义,都可以概括为求平均变化率的极限.【设计意图】给学生创设探究的平台,分析瞬时速度和切线的斜率两个具体问题,讨论解决这两个问题的方法、本质、思想上有什么共同之处,引导学生分析、观察、归纳,打通揭示事物本质的思维通道.教学环节内容师生活动设计意图类②类比迁移形成概念【思考】考虑求一般函数y=f(x)在点0x到0x+x之间的平均变化率的极限问题,也就是引导学生利用求瞬时速度的方法和思想类比探究,猜想得出函数在点0x处的变化率xyx0lim用具体到抽象,特殊到一般的思维方式,23比探索形成概念怎样计算函数在点0x处的变化率?引出导数定义后,回归问题情景,反思概念的“原型”解释“切线的斜率”、“物体的瞬时速度”的本质.=xxfxxfx)()(lim000,并对猜想的合理性进行分析后,引出定义1:(函数在一点处可导及其导数)利用瞬时速度进行类比迁移,自然引出函数在一点处可导和导数的概念.由具体到抽象再回到具体的过程,感知上升到了理性,强化了对概念的理解.类比探索形③剖析概念加深理解【探讨1】怎样判断函数在一点是否可导?判断函数)(xfy在点0x处是否可导判断极限xxfxxfx)()(lim000是否存在【探讨2】导数是什么?组织学生阅读“导数”定义,抓住定义中的关键词“可导”与“导数”交流探讨,然后通过师生互动挖掘这些概念之间的深层含义.引导学生以数学语言(文字语言、符号语言、图形语言)的理解、把握、运用为切入点去揭示概念的内涵与外延,提高学生数学阅3转化4成概念描述角度本质文字语言瞬时变化率符号语言0limxxy图形语言(切线斜率)分析导数的本质后,同时简单提及导数产生的时代背景.读和自主学习的能力.让学生感受数学文化的熏陶,了解导数的文化价值、科学价值和应用价值.教学环节内容师生活动设计意图类比探索形成概念【探讨3】求导数的方法是什么?...