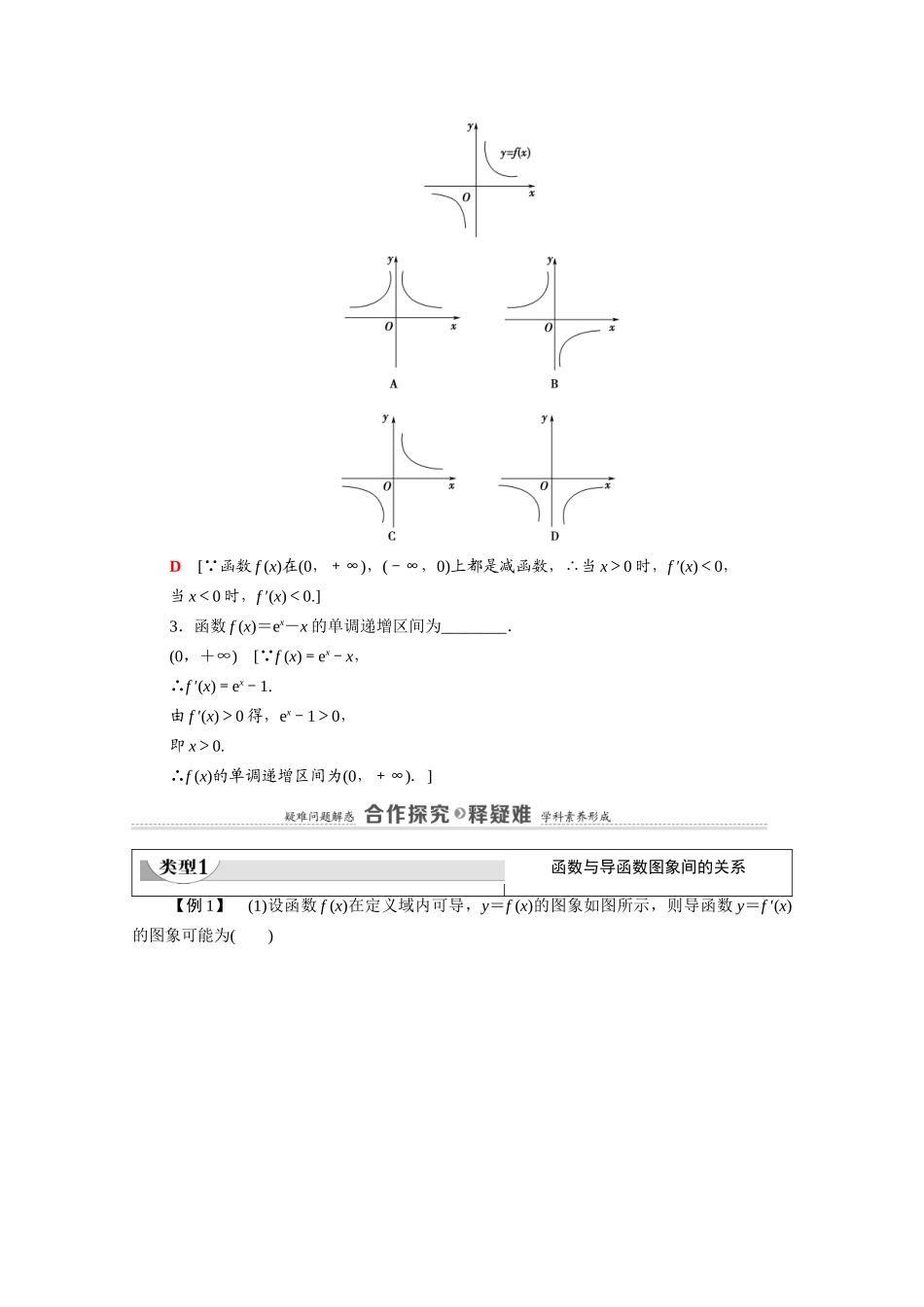
1.3导数在研究函数中的应用1.3.1函数的单调性与导数学习目标核心素养1.理解导数与函数的单调性的关系.(易混点)2.掌握利用导数判断函数单调性的方法.(重点)3.会用导数求函数的单调区间.(重点、难点)1.通过函数的单调性与其导数正负关系的学习,培养学生的逻辑推理、直观想象的核心素养.2.借助利用导数研究函数的单调性问题,提升学生的数学运算及逻辑推理的核心素养.1.函数的单调性与其导数正负的关系定义在区间(a,b)内的函数y=f(x):f′(x)的正负f(x)的单调性f′(x)>0单调递增f′(x)<0单调递减思考:如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?[提示]f(x)是常数函数.2.函数图象的变化趋势与导数值大小的关系一般地,设函数y=f(x),在区间(a,b)上:导数的绝对值函数值变化函数的图象越大快比较“陡峭”(向上或向下)越小慢比较“平缓”(向上或向下)1.函数f(x)=x+lnx在(0,6)上是()A.单调增函数B.单调减函数C.在上是减函数,在上是增函数D.在上是增函数,在上是减函数A[ x∈(0,6)时,f′(x)=1+>0,∴函数f(x)在(0,6)上单调递增.]2.函数y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能是()D[ 函数f(x)在(0,+∞),(-∞,0)上都是减函数,∴当x>0时,f′(x)<0,当x<0时,f′(x)<0.]3.函数f(x)=ex-x的单调递增区间为________.(0,+∞)[ f(x)=ex-x,∴f′(x)=ex-1.由f′(x)>0得,ex-1>0,即x>0.∴f(x)的单调递增区间为(0,+∞).]函数与导函数图象间的关系【例1】(1)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为()(2)已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是()(1)D(2)D[(1)由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.(2)从f′(x)的图象可以看出,在区间内,导数单调递增;在区间内,导数单调递减.即函数f(x)的图象在内越来越陡,在内越来越平缓,由此可知,只有选项D符合.]研究函数与导函数图象之间关系的方法研究一个函数的图象与其导函数图象之间的关系时,注意抓住各自的关键要素,对于原函数,要注意其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,则应注意其函数值在哪个区间内大于零,在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.[跟进训练]1.已知y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数)下面四个图象中,y=f(x)的图象大致是()C[当0<x<1时,xf′(x)<0,∴f′(x)<0,故f(x)在(0,1)上为减函数;当x>1时,xf′(x)>0,∴f′(x)>0,故y=f(x)在(1,+∞)上为增函数.故选C.]利用导数求函数的单调区间角度1不含参数的函数求单调区间【例2】求下列函数的单调区间.(1)f(x)=3x2-2lnx;(2)f(x)=x2·e-x;(3)f(x)=x+.[解](1)函数的定义域为D=(0,+∞). f′(x)=6x-,令f′(x)=0,得x1=,x2=-(舍去),用x1分割定义域D,得下表:xf′(x)-0+f(x)↘↗∴函数f(x)的单调递减区间为,单调递增区间为.(2)函数的定义域为D=(-∞,+∞). f′(x)=(x2)′e-x+x2(e-x)′=2xe-x-x2e-x=e-x(2x-x2),令f′(x)=0,由于e-x>0,∴x1=0,x2=2,用x1,x2分割定义域D,得下表:x(-∞,0)0(0,2)2(2,+∞)f′(x)-0+0-f(x)↘↗↘∴f(x)的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2).(3)函数的定义域为D=(-∞,0)∪(0,+∞). f′(x)=1-,令f′(x)=0,得x1=-1,x2=1,用x1,x2分割定义域D,得下表:x(-∞,-1)-1(-1,0)(0,1)1(1,+∞)f′(x)+0--0+f(x)↗↘↘↗∴函数f(x)的单调递减区间为(-1,0)和(0,1),单调递增区间为(-∞,-1)和(1,+∞).角度2含参数的函数的单调区间【例3】讨论函数f(x)=ax2+x-(a+1)lnx(a≥0)的单调性.思路探究:―→――――――――→―→[解]函数f(x)的定义域为(0,+∞),f′(x)=ax+1-=.(1)当a=0时,f′(x)=,由f′(x)>0,得x>1,由f′(x)<0,得0<x<1.∴f(x)在(0,1)内为减函数,在(1,+∞)内...