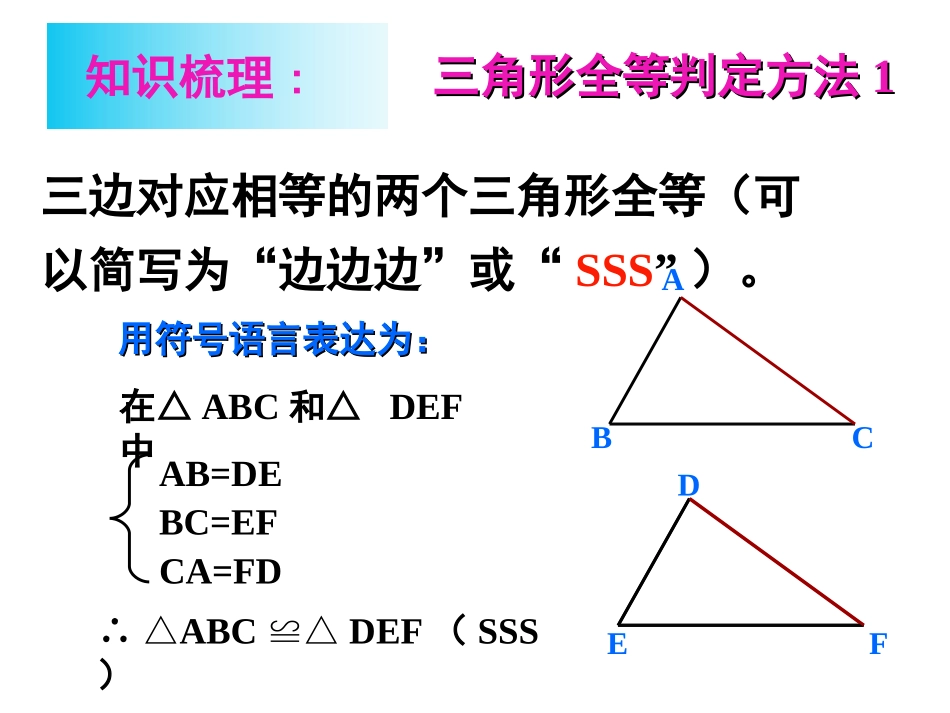
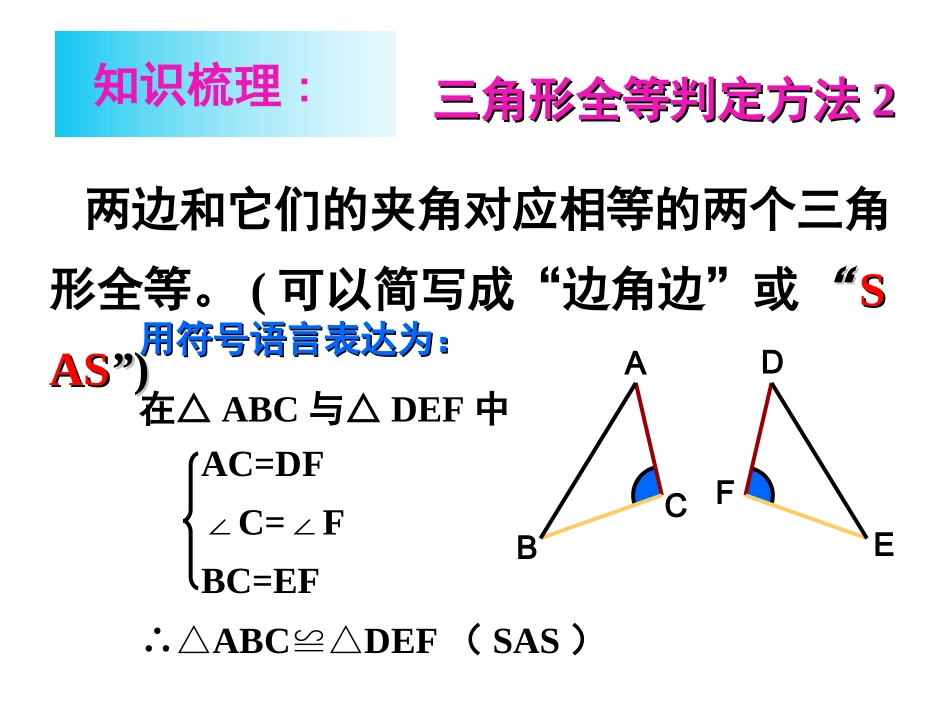
全等三角形的判定综合(1)三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCDEF在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FD用符号语言表达为:用符号语言表达为:三角形全等判定方法三角形全等判定方法11知识梳理:三角形全等判定方法三角形全等判定方法22用符号语言表达为:用符号语言表达为:在△ABC与△DEF中∴△ABCDEF≌△(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或““SSASAS””))知识梳理:FEDCBAAC=DF∠C=F∠BC=EF∠A=D∠(已知)AB=DE(已知)∠B=E∠(已知)在△ABC和△DEF中∴△ABCDEF≌△(ASA)有两角和它们夹边对应相等的两个三角形有两角和它们夹边对应相等的两个三角形全等全等((可以简写成“角边角”或“可以简写成“角边角”或“ASASAA””)。)。用符号语言表达为:用符号语言表达为:FEDCBA三角形全等判定方法三角形全等判定方法33知识梳理:知识梳理:三角形全等判定方法三角形全等判定方法44有两角和其中一个角的对边对应相等的两个三角有两角和其中一个角的对边对应相等的两个三角形全等形全等((可以简写成“角边角”或“可以简写成“角边角”或“AAAASS””)。)。CBAFED知识梳理:DCBAABDABCABDABCSSASSA不不能判定全能判定全等等二、几种常见全等三角形基本图形二、几种常见全等三角形基本图形FEDCBAFEDCBAFEDCBA平移EDCBAEDCBA旋转EDCBADCBADCBAEDCBAOEDCBA翻折例1、如图,已知∠B=∠DEF,AB=DE,要说明△ABCDEF≌△,(1)若以“SAS”为依据,还须添加的一个条件为;(2)若以“ASA”为依据,还须添加的一个条件为;(3)若以“AAS”为依据,还须添加的一个条件为.ABCFEDBC=EF∠A=∠D∠ACB=∠F例例2:2:如图如图,,点点BB在在AEAE上上,CAB=DAB,∠∠,CAB=DAB,∠∠要使要使ΔABC≌ΔABC≌ΔABD,ΔABD,可补充的一个条件是可补充的一个条件是..EDCBA分析:已知分析:已知AA→CA∠→CA∠B=DAB∠B=DAB∠①①用用SAS,SAS,需要补充条需要补充条件件AD=AC,AD=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠CBA=DBA,∠CBA=DBA,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠C=D,∠C=D,∠④④此外此外,,补充条件补充条件∠∠CBCBE=DBE∠E=DBE∠也可以也可以(?)(?)SASSASASAASAAASAASSS→AB=AB(→AB=AB(公共边公共边).).例3、已知:AB=CD,AD=CB.试说明∠A=C∠。CDABO例4、已知:如图,BE、CF是△ABC的高,分别在射线BE与CF上取点P与Q,ABCEFPQ使BP=AC,CQ=AB.求证:(1)AQ=AP(2)APAQ⊥