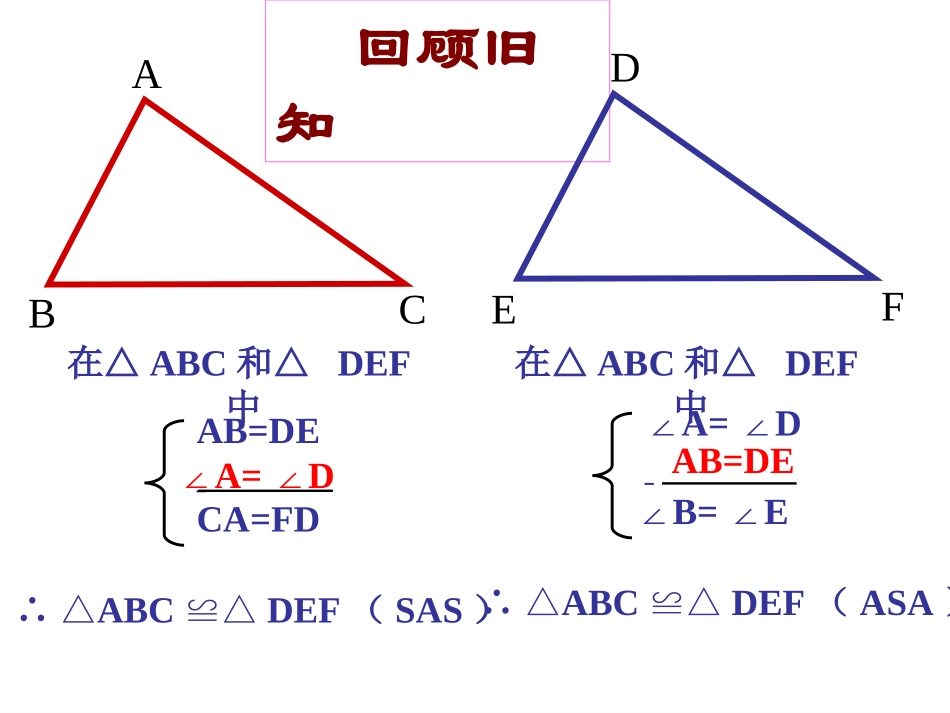
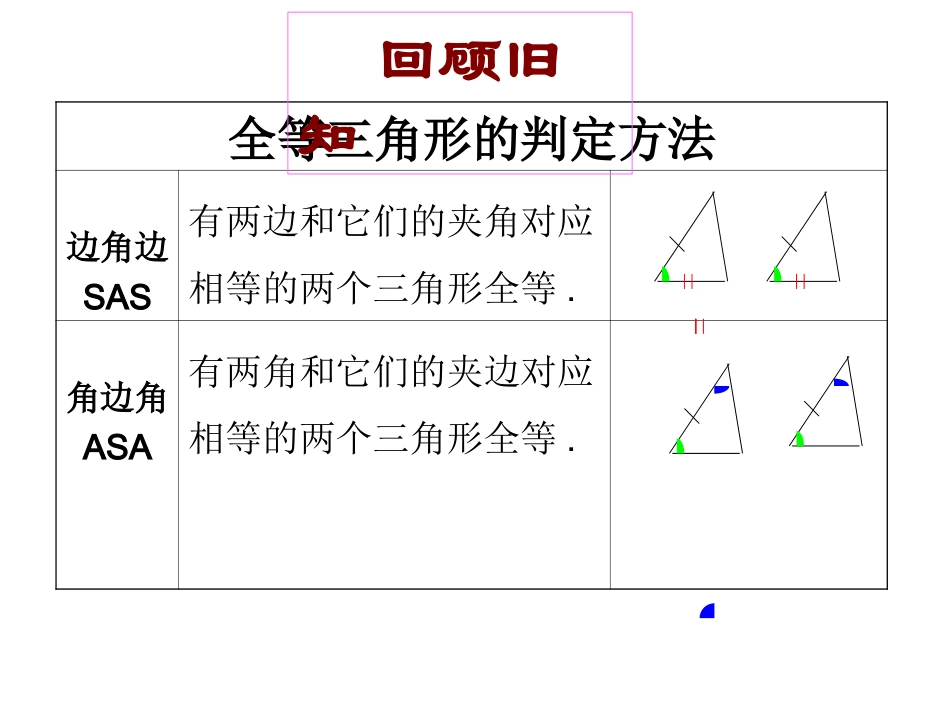
全等三角形的判定全等三角形的判定AAS回顾旧知ABCDE在△ABC和△DEF中∴△ABCDEF≌△(SAS)AB=DECA=FD在△ABC和△DEF中∠A=D∠∠B=E∠∴△ABCDEF≌△(ASA)F∠A=D∠AB=DE全等三角形的判定方法边角边SAS有两边和它们的夹角对应相等的两个三角形全等.角边角ASA有两角和它们的夹边对应相等的两个三角形全等.回顾旧知两边分别相等且其一组等边的对角相等的两个三角形不一定全等3cm2.5cm2.5cm3cm45°45°两角一夹边(ASA)两角一对边(AAS)?引入新课学习目标1.掌握三角形全等的“角角边”定理.2.能根据条件选择合适的判定进行推理论证。△ABC与△DEF中,AB=DE,A=D,∠∠C=F.∠∠CABFDE预习反馈CAB角角边公理:两角分别相等及其中一组等角的对边也相等的两个三角形全等.(AAS)FDE预习反馈△ABC与△DEF中,AB=DE,∠A=D,∠∠C=F.∠∴△ABCDEF≌△(AAS)证明:在△ADC和△AEB中,∠1=∠2(已知)∠A=A∠(公共角)AD=AE(已知)∴△ADCAEB≌△(AAS)1、书P82练习第1题已知:AD=AE,∠1=∠2,求证:△ADC≌△AEBABDCE理解与应用121、书P82练习第1题已知:AD=AE,∠1=∠2,求证:△ADC≌△AEBABDCE理解与应用12∠D=∠EAC=AB1、书P82练习第1题已知:AD=AE,∠1=∠2,求证:△ADC≌△AEBABDCE交流合作12图形中有几组全等的三角形,并写出证明过程(1)每组板书一种解题方法,参考其他组尽量板书不同的方法;(2)比一比哪组解题方法多,没有板书可以口述;(3)比较所以的解题方法,哪种最简单。全等三角形的判定方法边角边SAS有两边和它们的夹角对应相等的两个三角形全等.角边角ASA角角边AAS有两角和它们的夹边对应相等的两个三角形全等.两角分别相等及其中一组等角的对边也相等的两个三角形全等课堂小结谢谢合作,再见!