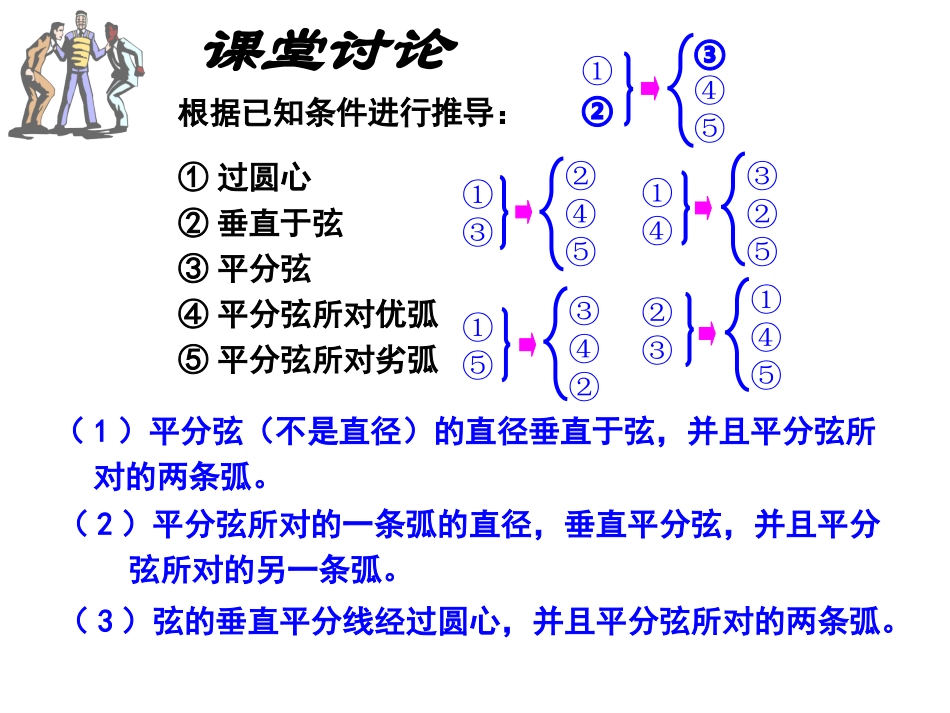
垂径定理定理垂直于弦的直径平分弦,并且平分弦所对的两条弧.●OABCDM└CDAB,⊥如图∵CD是直径,∴AM=BM,⌒⌒AC=BC,⌒⌒AD=BD.推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。课堂讨论根据已知条件进行推导:①过圆心②垂直于弦③平分弦④平分弦所对优弧⑤平分弦所对劣弧(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。①⑤③④②①④③②⑤①③②④⑤①④⑤②③(3)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。(2)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。①②③④⑤三个命题命题一:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。命题三:弦的垂直平分线经过圆心,并且平分弦所对的两条弧。命题二:平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧。.OAEBDC已知:AB是弦,CD平分AB,CDA⊥B。求证:CD是直径,AD=BD,AC=BC⌒⌒⌒⌒已知:CD是直径,AB是弦,并且CD平分AB。求证:CDAB⊥,AD=BD,AC=BC已知:CD是直径,AB是弦,并且AD=BD(AC=BC)。求证:CD平分AB,AC=BC(AD=BD)CDAB⊥⌒⌒⌒⌒⌒⌒⌒⌒⌒⌒⌒⌒根据垂径定理与推论可知:对于一个圆和一条直线来说,如果具备:那么,由五个条件中的任何两个条件都可以推出其他三个结论。注意要点①经过圆心②垂直于弦③平分弦④平分弦所对的优弧⑤平分弦所对的劣弧1.过⊙o内一点M的最长的弦长为10㎝,最短弦长为8㎝,那么⊙o的半径是2.已知⊙o的弦AB=6㎝,直径CD=10㎝,且AB⊥CD,那么C到AB的距离等于3.已知⊙O的弦AB=4㎝,圆心O到AB的中点C的距离为1㎝,那么⊙O的半径为4.如图,在⊙O中弦AB⊥AC,OM⊥AB,ON⊥AC,垂足分别为M,N,且OM=2,0N=3,则AB=,AC=,OA=BAMCON5㎝1㎝或9㎝56413Cm3cm1、已知P为内一点,且OP=2cm,如果的半径是,则过P点的最长的弦等于.最短的弦等于_________。⊙o⊙o随堂训练OAPBNM2、已知直径AB被弦CD分成AE=4,EB=8,CD和AB成300角,则弦CD的弦心距OF=____;CD=_____.1352EOABCDF3、同心圆中,大圆的弦AB交小圆于C,D,已知AB=4,CD=2,AB的弦心距为1,则两个同心圆的半径之比为()A.3:2B.:C.:2D.5:4525B4、如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心,则折痕AB的长为()A.2cmB.cmC.cmD.cm33252C5、已知点P是半径为5的⊙O内的一定点,且OP=4,则过P点的所有弦中,弦长可能取的整数值为()A.5,4,3B.10,9,8,7,6,5,4,3C.10,9,8,7,6D.10,9,8COBA6、已知:⊙O中弦AB∥CD且AB=9cm,CD=12cm,⊙O的直径为15cm,则弦AB,CD间的距离为()A.1.5cmB.10.5cm;C.1.5cm或10.5cmD.都不对;CABCDO7.(2007.江西)如图,点A、B是⊙O上两点,AB=10,点P是⊙O上的动点,(P与A,B不重合),连接AP、PB,过点O分别OE⊥AP于E,OF⊥PB于F,则EF=——。5OFEPBA8、如图,有一圆弧形桥拱,拱形的半径为10米,桥拱的跨度AB=16米,则拱高为米。AB·CD4O5.如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB=24cm,则截面上有油部分油面高CD=——————半径、弦长、弓形的高、圆心到弦的距离知二求二8cmODCBA9、在直径为650mm的圆柱形油槽内装入一些油后,截面的油面宽AB=600mm,求油的最大深度.BAO600ø650DCBAOED┌600CD10、已知:AB是⊙O的直径,CD是弦,AE⊥CD于E,BF⊥CD于F.求证:EC=DF.AOGBFCDEOACDEFBG垂径定理的应用G.AOBECDFOABCDGEF