高数课件14凹凸性VIP免费

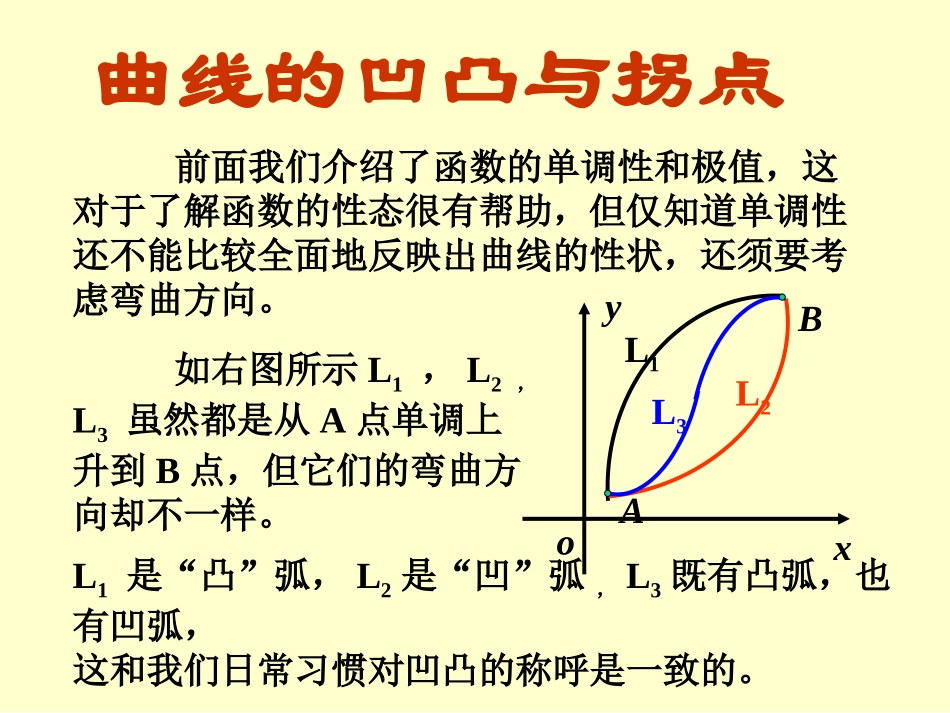
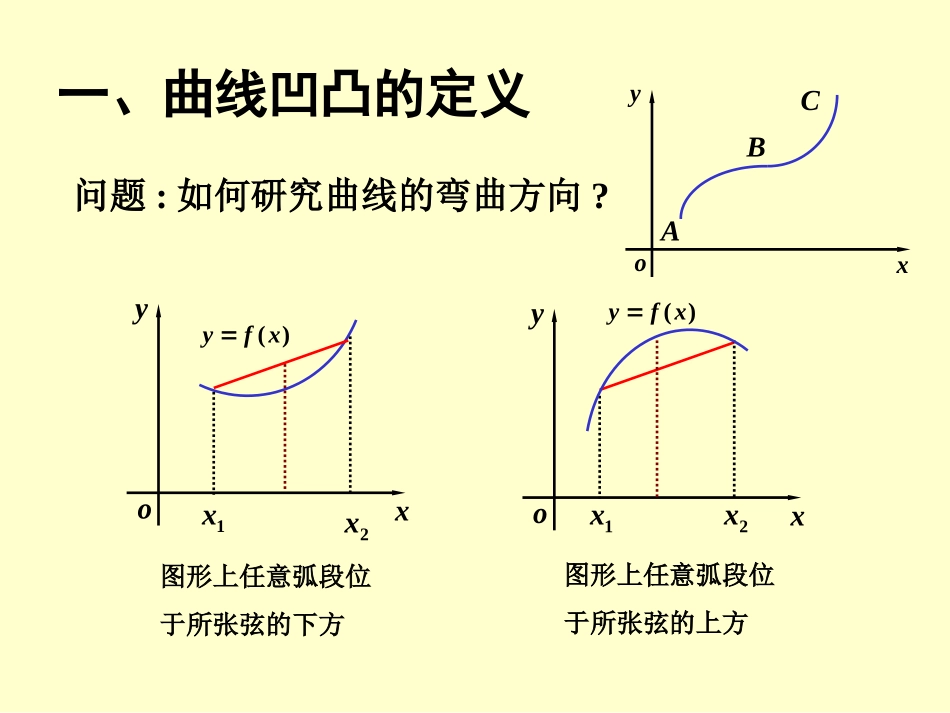
曲线的凹凸与拐点前面我们介绍了函数的单调性和极值，这对于了解函数的性态很有帮助，但仅知道单调性还不能比较全面地反映出曲线的性状，还须要考虑弯曲方向。oyxL3L2L1AB如右图所示L1，L2，L3虽然都是从A点单调上升到B点，但它们的弯曲方向却不一样。L1是“凸”弧，L2是“凹”弧，L3既有凸弧，也有凹弧，这和我们日常习惯对凹凸的称呼是一致的。一、曲线凹凸的定义问题:如何研究曲线的弯曲方向?xyoxyo1x2x)(xfy图形上任意弧段位于所张弦的上方xyo)(xfy1x2x图形上任意弧段位于所张弦的下方ABC定义;),()(,2)()()2(,,),(,),()(212121内的图形是凹的在那末称恒有两点内任意如果对内连续在设baxfxfxfxxfxxbabaxf;),()(,2)()()2(,,),(212121内的图形是凸的在那末称恒有内任意两点如果对baxfxfxfxxfxxba;)(],[)(,)(),(,],[)(的或凸内的图形是凹在那末称的或凸内的图形是凹且在内连续在如果baxfbabaxf二、曲线凹凸的判定xyo)(xfyxyo)(xfyabAB递增)(xfabBA0y递减)(xf0y定理1.],[)(,0)()2(;],[)(,0)()1(),(,),(,],[)(上的图形是凸的在则上的图形是凹的在则内若在二阶导数内具有在上连续在如果baxfxfbaxfxfbababaxf证明2121),,(,)2(xxbaxx0210210,2xxxxhxxx记上在对],[],,[)(2001xxxxxf分别应用L—定理，得hfxfxf)()()(110)(011xxhfxfxf)()()(202)(220xx两式相减，得hffxfxfxf)]()([)]()([)(221210由假设0)(xf内单调减在],[)(baxf0)()(2121ff由0)]()([)(2210xfxfxf2)()(22121xfxfxxf即这就证明了内是上凸的在),()(baxf同理可证（1）注定理的结论可推广到任意区间上例1.3的凹凸性判断曲线xy解,32xy,6xy时，当0x,0y为凸的；在曲线]0,(时，当0x,0y为凹的；在曲线),0[.)0,0(点是曲线由凸变凹的分界点注意到,三、曲线的拐点及其求法连续曲线上凹凸的分界点称为曲线的拐点.定理2如果)(xf在),(00xx内存在二阶导数,则点)(,00xfx是拐点的必要条件是0)(0"xf.1.定义注意:拐点处的切线必在拐点处穿过曲线.2.拐点的求法证,)(二阶可导xf,)(存在且连续xf,])([)(0两边变号在则xxfxf,))(,(00是拐点又xfx,)(0取得极值在xxf,条件由可导函数取得极值的.0)(xf方法1:,0)(,)(00xfxxf且的邻域内二阶可导在设函数;))(,(,)()1(000即为拐点点变号两近旁xfxxfx.))(,(,)()2(000不是拐点点不变号两近旁xfxxfx例2.14334凹、凸的区间的拐点及求曲线xxy解),(:D,121223xxy).32(36xxy,0y令.32,021xx得x)0,(),32()32,0(032)(xf)(xf00凹的凸的凹的拐点拐点)1,0()2711,32().,32[],32,0[],0,(凹凸区间为方法2:.)())(,(,0)(,0)(,)(00000的拐点线是曲那末而且的邻域内三阶可导在设函数xfyxfxxfxfxxf例3.)]2,0([cossin的拐点内求曲线xxy解,sincosxxy,cossinxxy.sincosxxy,0y令.47,4321xx得2)43(f,02)47(f,0内曲线有拐点为在]2,0[).0,47(),0,43(.)())(,(,)(000的拐点是连续曲线也可能点不存在若xfyxfxxf注意:例4假定f(x)在x=x0处具有直到n阶的连续导数，且0)(,0)()()(0)(0)1(00xfxfxfxfnn但这里n为奇数≥3，是拐点则))(,(00xfx证)()(xfxg记0)()(0)(0)3(xfxgnn则由高阶导数判定极值的方法知处取得极值在0)(xxg不妨设为极小值的左、右两侧邻近，有在0x0)()(0xfxf)(xf时0xx0)()(0xfxf时0xx0)()(0xfxf二阶导数变号，是拐点则))(,(00xfx例5.3的拐点求曲线xy解,0时当x,3132xy,9435xy.,,0均不存在是不可导点yyx,0,)0,(y内但在;]0,(上是凹的曲线在,0,),0(y内在.),0[上是凸的曲线在.)0,0(3的拐点是曲线点xy例6求曲线...