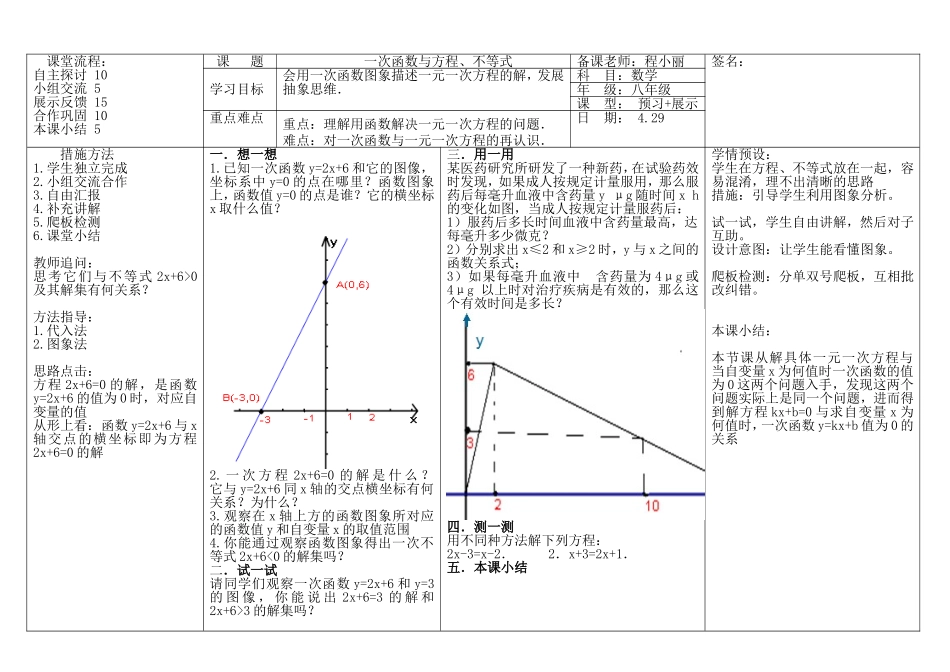
课堂流程:自主探讨10小组交流5展示反馈15合作巩固10本课小结5课题一次函数与方程、不等式备课老师:程小丽签名:学习目标会用一次函数图象描述一元一次方程的解,发展抽象思维.科目:数学年级:八年级课型:预习+展示重点难点重点:理解用函数解决一元一次方程的问题.难点:对一次函数与一元一次方程的再认识.日期:4.29措施方法1.学生独立完成2.小组交流合作3.自由汇报4.补充讲解5.爬板检测6.课堂小结教师追问:思考它们与不等式2x+6>0及其解集有何关系?方法指导:1.代入法2.图象法思路点击:方程2x+6=0的解,是函数y=2x+6的值为0时,对应自变量的值从形上看:函数y=2x+6与x轴交点的横坐标即为方程2x+6=0的解一.想一想1.已知一次函数y=2x+6和它的图像,坐标系中y=0的点在哪里?函数图象上,函数值y=0的点是谁?它的横坐标x取什么值?2.一次方程2x+6=0的解是什么?它与y=2x+6同x轴的交点横坐标有何关系?为什么?3.观察在x轴上方的函数图象所对应的函数值y和自变量x的取值范围4.你能通过观察函数图象得出一次不等式2x+6<0的解集吗?二.试一试请同学们观察一次函数y=2x+6和y=3的图像,你能说出2x+6=3的解和2x+6>3的解集吗?三.用一用某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定计量服用,那么服药后每毫升血液中含药量yμg随时间xh的变化如图,当成人按规定计量服药后:1)服药后多长时间血液中含药量最高,达每毫升多少微克?2)分别求出x≤2和x≥2时,y与x之间的函数关系式;3)如果每毫升血液中含药量为4μg或4μg以上时对治疗疾病是有效的,那么这个有效时间是多长?四.测一测用不同种方法解下列方程:2x-3=x-2.2.x+3=2x+1.五.本课小结学情预设:学生在方程、不等式放在一起,容易混淆,理不出清晰的思路措施:引导学生利用图象分析。试一试,学生自由讲解,然后对子互助。设计意图:让学生能看懂图象。爬板检测:分单双号爬板,互相批改纠错。本课小结:本节课从解具体一元一次方程与当自变量x为何值时一次函数的值为0这两个问题入手,发现这两个问题实际上是同一个问题,进而得到解方程kx+b=0与求自变量x为何值时,一次函数y=kx+b值为0的关系D