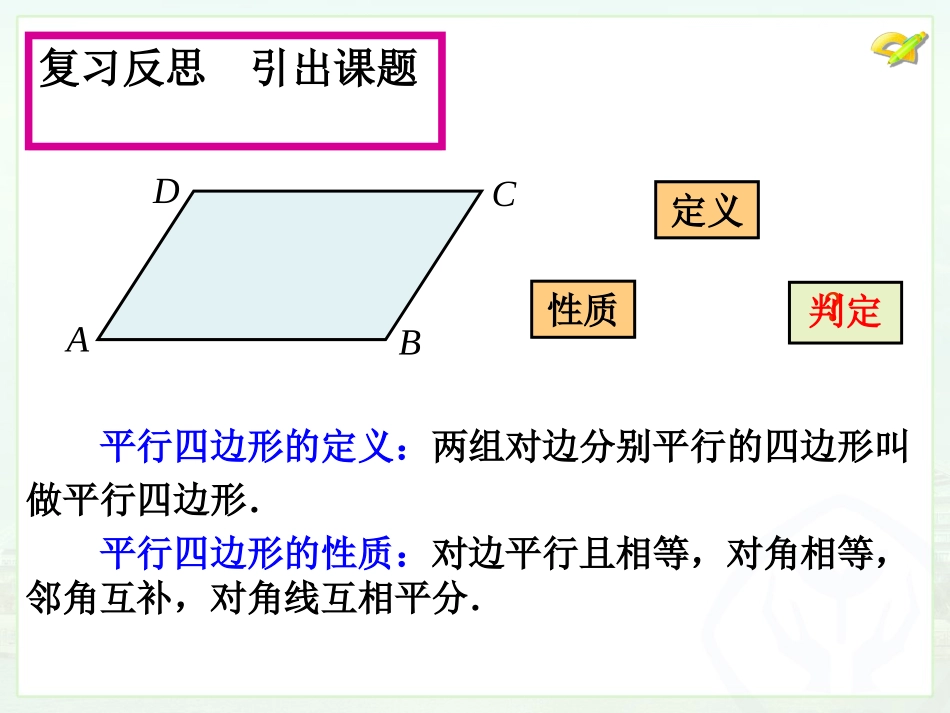
八年级下册18.1.2平行四边形的判定(1)广州市第九十七中学•学习目标:1.经历平行四边形判定定理的猜想与证明过程,体会探究图形判定的一般思路;2.掌握平行四边形的四个判定定理,对平行四边形的判定做进一步的探索.•学习重点:平行四边形判定定理的探究.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.平行四边形的性质:对边平行且相等,对角相等,邻角互补,对角线互相平分.?判定性质定义复习反思引出课题DABC判定性质定义复习反思引出课题DABC问题如何寻找平行四边形的判定方法?证明:连接BD.∵AB=CD,AD=BC,BD是公共边,∴△ABD≌△CDB.∴∠1=∠2,∠3=∠4.∴AB∥DC,AD∥BC.∴四边形ABCD是平行四边形.如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.演绎推理形成定理两组对边分别相等的四边形是平行四边形.判定定理1猜想1DABC1234证明:∵多边形ABCD是四边形,∴∠A+∠B+∠C+∠D=360°.又∵∠A=∠C,∠B=∠D,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥DC.∴四边形ABCD是平行四边形.如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.演绎推理形成定理两组对角分别相等的四边形是平行四边形.判定定理2猜想2DABC如图,在四边形ABCD中,AC,BD相交于点O,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形.演绎推理形成定理对角线互相平分的四边形是平行四边形.判定定理3DABCO猜想3证明:∵OA=OC,OB=OD,∠AOD=∠COB,∴△AOD≌△COB.∴∠OAD=∠OCB.∴AD∥BC.同理AB∥DC.∴四边形ABCD是平行四边形.如图,在四边形ABCD中,AD∥BC,AD=BC.求证:四边形ABCD是平行四边形.演绎推理形成定理一组对边平行且相等的四边形是平行四边形.判定定理4猜想4证明:连接BD.∵AD∥BC,∴∠ADB=∠CBD.又∵AD=BC,BD=DB,∴△ABD≌△CDB.∴AB=CD.又∵AD=BC∴四边形ABCD是平行四边形.DABC两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形.从角考虑两组对角分别相等的四边形是平行四边形.从对角线考虑对角线互相平分的四边形是平行四边形.从边考虑课堂小结现在,我们一共有哪些判定平行四边形的方法呢?平行四边形的判定定理与相应的性质定理互为逆定理。证明:∵AD∥BC,∴∠A+∠B=180°.又∵∠B=∠D,∴∠A+∠D=180°,∴AB∥DC.又∵AD∥BC,∴四边形ABCD是平行四边形.如图,在四边形ABCD中,AD∥BC,∠B=∠D.四边形ABCD是平行四边形吗?平行四边形判定的进一步探索一组对边平行,一组对角相等的四边形是平行四边形吗?猜想5DABC反例:如图已知:在四边形ABCD中,AB∥DC,AD=BC四边形ABCD是平行四边形吗?平行四边形判定的进一步探索一组对边平行,另一组对边相等的四边形是平行四边形吗?猜想6DCAB如图,在四边形ABCD中,AD=BC,∠A=∠C.四边形ABCD是平行四边形吗.平行四边形判定的进一步探索一组对边相等,一组对角相等的四边形是平行四边形吗?猜想7EDABCDCAB(E)课堂小结过程与方法的角度:研究图形的一般思路.性质定义判定逆向猜想这个研究过程揭示了定义、性质、判定之间的逻辑关系,提供了研究几何图形的一般思路.平行四边形的判定定理与相应的性质定理互为逆定理。