二次根式的乘除法(第二课时)VIP免费

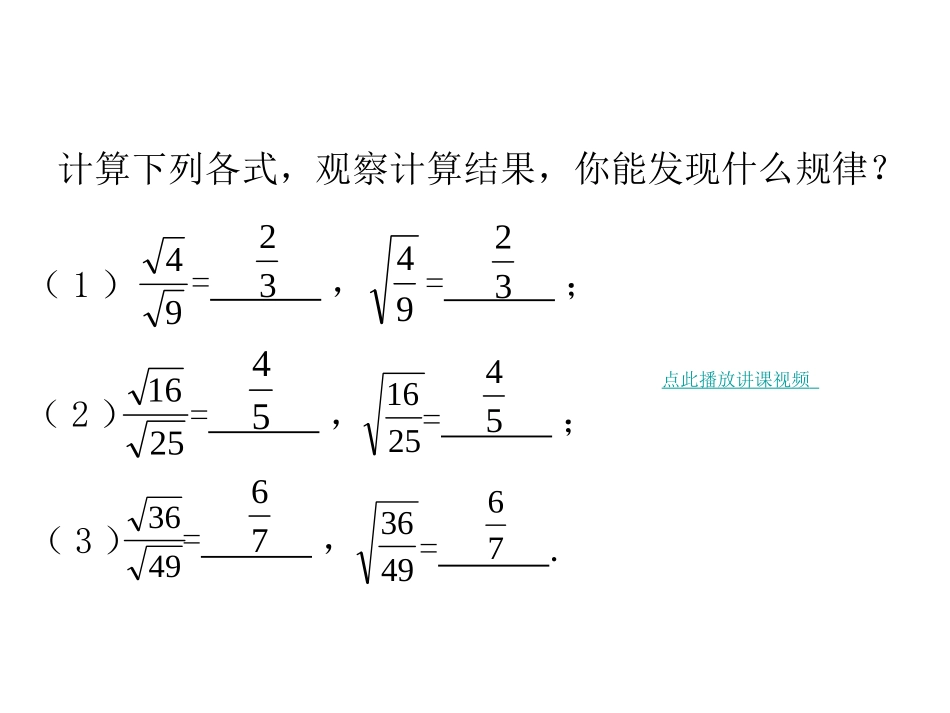
16.2二次根式的乘除（第2课时）八年级下册点此播放教学视频复习提问1.二次根式的乘法法则：00baabba，即：两个非负数算术平方根的积等于这两个数积的算术平方根.乘法法则是如何得出的？除法有没有类似的法则？2.乘法公式的逆用：00babaab，有何作用？即：积的算术平方根等于各因式的算术平方根的积.探究（1）计算下列各式，观察计算结果，你能发现什么规律？32（1）=，=；9494（2）=；=，25162516=，（3）=.493649365476325476点此播放讲课视频探究（1）二次根式的除法法则是：00bababa，.即：商的算术平方根等于算术平方根的商.二次根式的除法法则是类比乘法法则，采用由特殊到一般的方法归纳得出的.应用（1）例1计算：（1）324；.（2）18123；解：22248324324（1）.（2）33931823181231812318123运算结果中应不含能开得尽方的因数或因式.探究（2）把二次根式的除法法则反过来，就得到：00bababa，，利用它可以进行二次根式的化简.例2化简：（1）；1003（2）.2775（1）；解：10310031003.（2）3535333527752222应用（2）例3计算：（1）；53；（2）2723.（3）a28.解：5155155155553535322（1）解法1：.解法2：5155155553532aa2先用除法法则运算，再用性质去掉分母中的根号利用分式的基本性质和公式去掉分母中的根号aa2应用（2）（2）.2723332333232236333232.（3）a28aaaaaaa2242228利用第（1）题中解法2的方法去掉分母中的根号.二次根式的运算中，最后结果分母一般不含二次根式.应用（2）例4计算：（1）107514；（2）6152112.被开方数为带分数的先化为假分数再进行运算解：（1）514623710521107521107521.应用（2）（2）56352623526123526123526152112.如果根号前有系数，就把系数相除，作为商的系数.最简二次根式上述几个例题中运算的最后结果，都有如下两个特点：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式；满足上述两个条件的二次根式，叫做最简二次根式.说明：二次根式的运算中，一般要把最后结果化为最简二次根式，并且分母中不含二次根式.应用例5设长方形的面积为S，相邻两边长分别为a，b.已知S=，b=，求a.3210解：因为S=ab，所以530101010321032bSa.注意本题中去掉分母中的根号的方法，是否还有其他方法呢？应用2212221212122hhhhhhhhhhRhR2122RhRh2212221212122hhhhhhhhhhRhR2122RhRh那么它们例6如果两个电视塔的高分别是2122RhRhh1km，h2km，的传播半径之比是.那么它们例6如果两个电视塔的高分别是2122RhRhh1km，h2km，的传播半径之比是.试化简该式.利用除法法则，分式的性质和二次根式的性质对代数式进行化简，从结果来看，这个比与地球半径无关，简化了解决问题的步骤.课堂小结一、本节课的主要内容是什么？二、运用二次根式的除法法则的关键问题是什么？四、本节课涉及的思想方法有哪些？三、学习最简二次根式有何意义？作业布置二、课外思考：化简：一、书面作业：练习第2题；习题第8、11题.(1)ab22；(2).2323