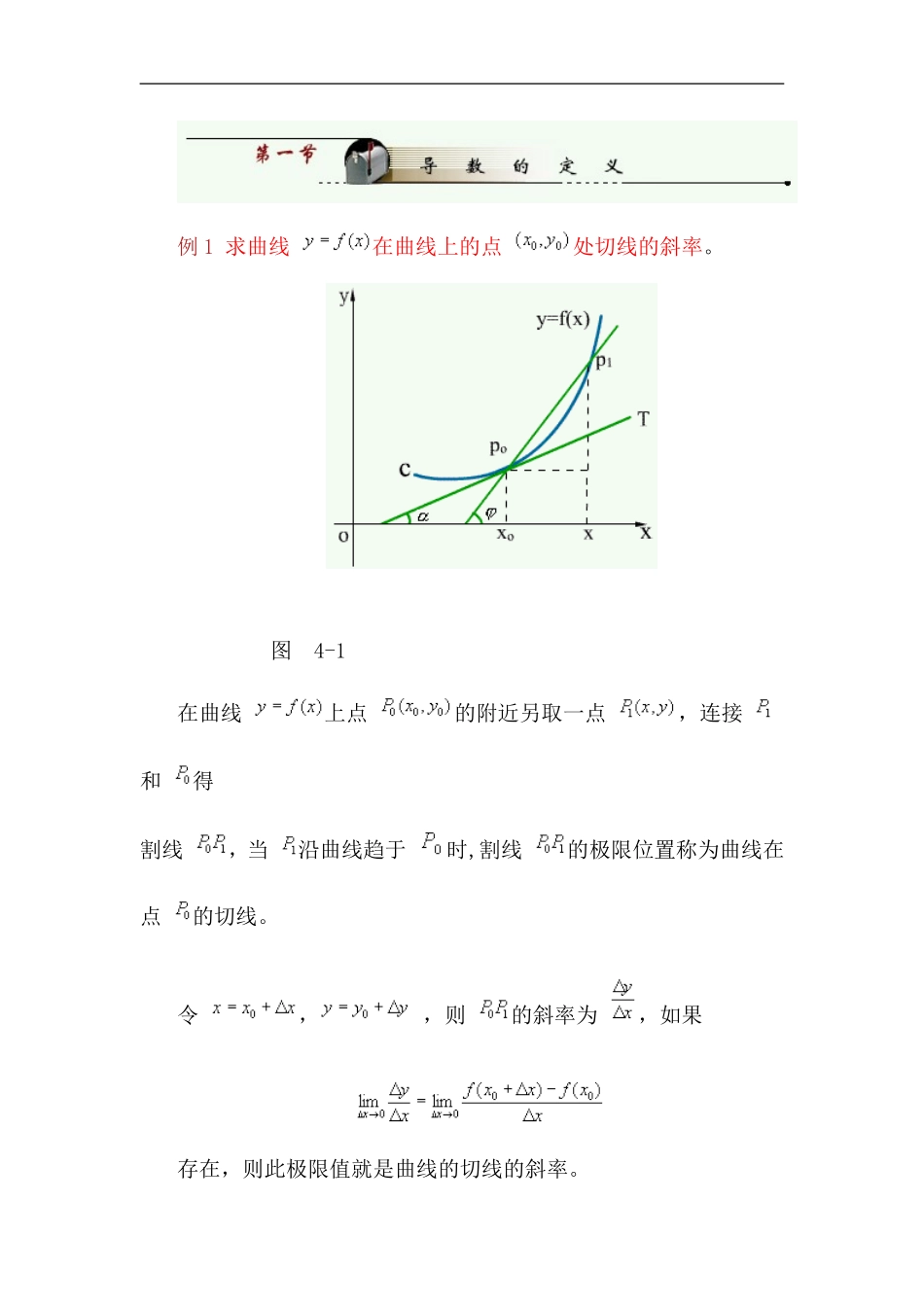
DDY整理例1求曲线在曲线上的点处切线的斜率。图4-1在曲线上点的附近另取一点,连接和得割线,当沿曲线趋于时,割线的极限位置称为曲线在点的切线。令,,则的斜率为,如果存在,则此极限值就是曲线的切线的斜率。DDY整理设切线的倾角为,则从另一角度,表示在区间(或)的平均变化率,极限称为函数在的变化率。例2求变速直线运动的物体的瞬时速度。物体产生的位移是时间的函数,设运动方程为,求在时刻的速度。定义设函数在点的邻域内有定义,当自变量从变到时,则函数得相应的增量,如果极限DDY整理存在,则称函数在点可导,并称此极限为函数在点的导数。记作,或,,,即如果记,则上式可写为或记则如果上述极限不存在,则称函数在点不可导。例3设在处可导(1)(2)则?解(1)DDY整理(2)例4设且则解例5证明:在处不可导。DDY整理解在处不可导。注意:函数在(0,0)处的切线存在,斜率为,所以函数在处有或时,有时也称在处导数无穷大。图4-2左、右导数左导数右导数DDY整理显然有,在处可导的充要条件是:在的左、右导数都存在且相等。例6讨论函数在处的可导性。解在可导且如果函数在区间内每一点都可导(闭区间时,左端点须右可导,右端点须左可导),则称函数在区间内可导,此时其导数值是随而变的函数,称为的导函数,简称导数,记作而是的导函数在处的函数值。DDY整理用定义求函数的导数(函数),可分三步进行:(1)求增量(2)求比值(3)求极限例7求(为正整数)解(应用二项式定理),所以一般地有为任意实数。例8求的导数。DDY整理解所以利用导数的定义和基本求导法则求出了常用初等函数的导数,列于书中141页公式表中,请大家背下来。如:,,,,,,,,,DDY整理,,,.例9设,求解定理如果函数在点可导,则函数在点连续。因为在点可导,即,(增量公式)即DDY整理所以时,。在处连续。注:定理的逆不一定成立。既函数在点连续,却不一定可导。例10函数,在点连续,但不可导。所以在连续。图4-3在处不可导。例11讨论函数DDY整理在处的连续性与可导性。解在处连续。在处可导,且。例12设问当为何值时,在连续且可导。解在处连续,则,在处可导,则DDY整理在点的导数是曲线在点处切线的斜率。所以在处的切线方程为法线方程为例13求在(-1,1)处的切线方程和法线方程。解,切线方程为法线方程为例14设曲线上的点处的切线平行于直线,DDY整理求点的坐标。解因为曲线在点的切线平行于,解出所以点的坐标为。