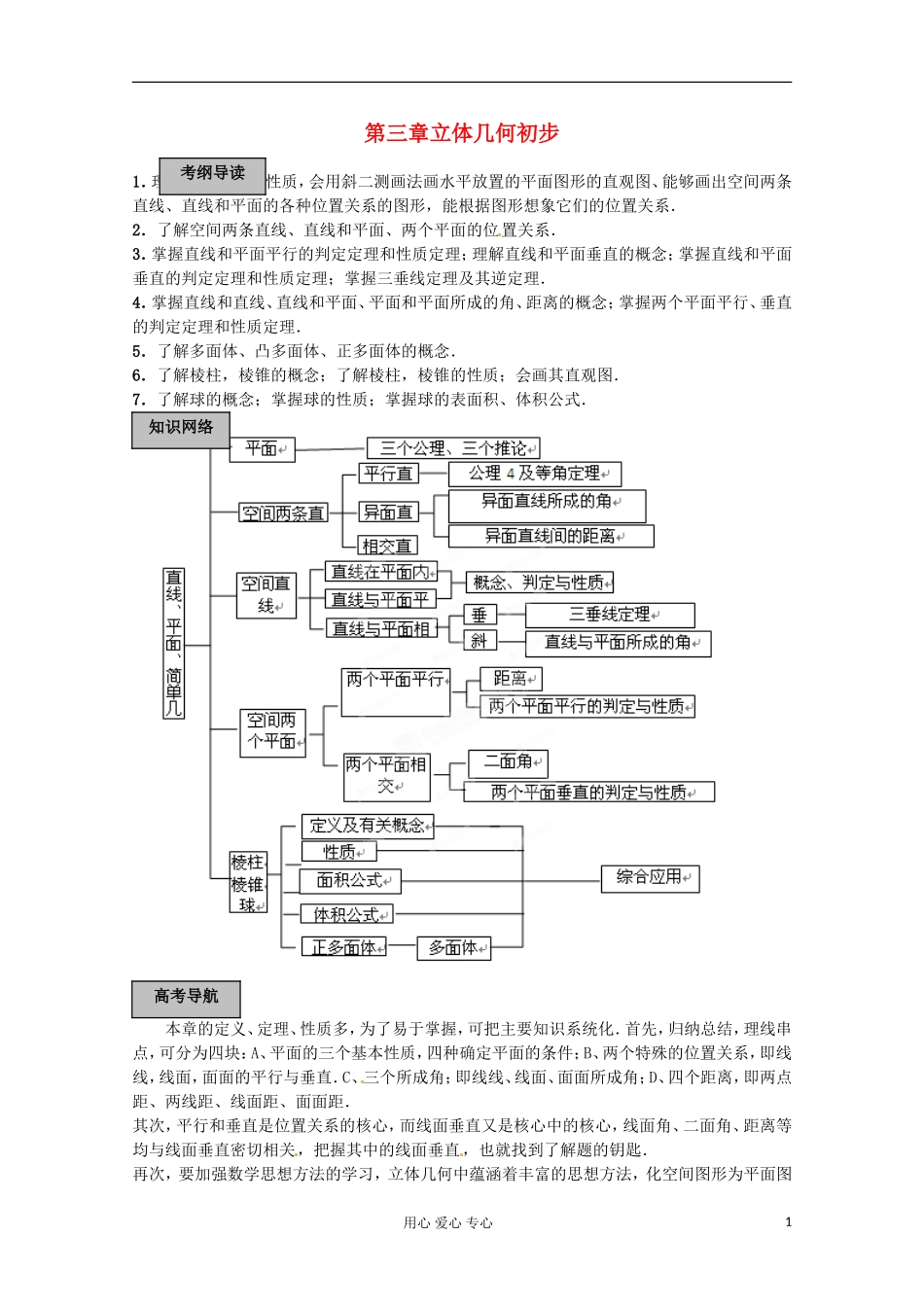
第三章立体几何初步1.理解平面的基本性质,会用斜二测画法画水平放置的平面图形的直观图、能够画出空间两条直线、直线和平面的各种位置关系的图形,能根据图形想象它们的位置关系.2.了解空间两条直线、直线和平面、两个平面的位置关系.3.掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念;掌握直线和平面垂直的判定定理和性质定理;掌握三垂线定理及其逆定理.4.掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念;掌握两个平面平行、垂直的判定定理和性质定理.5.了解多面体、凸多面体、正多面体的概念.6.了解棱柱,棱锥的概念;了解棱柱,棱锥的性质;会画其直观图.7.了解球的概念;掌握球的性质;掌握球的表面积、体积公式.本章的定义、定理、性质多,为了易于掌握,可把主要知识系统化.首先,归纳总结,理线串点,可分为四块:A、平面的三个基本性质,四种确定平面的条件;B、两个特殊的位置关系,即线线,线面,面面的平行与垂直.C、三个所成角;即线线、线面、面面所成角;D、四个距离,即两点距、两线距、线面距、面面距.其次,平行和垂直是位置关系的核心,而线面垂直又是核心中的核心,线面角、二面角、距离等均与线面垂直密切相关,把握其中的线面垂直,也就找到了解题的钥匙.再次,要加强数学思想方法的学习,立体几何中蕴涵着丰富的思想方法,化空间图形为平面图用心爱心专心1知识网络考纲导读高考导航形解决,化几何问题为坐标化解决,自觉地学习和运用数学思想方法去解题,常能收到事半功倍的效果.第1课时平面的基本性质例1.正方体ABCD-A1B1C1D1中,对角线A1C与平面BDC1交于O,AC、BD交于点M.求证:点C1、O、M共线.证明:A1A∥CC1确定平面A1CA1C面A1CO∈面A1CO∈A1C面BC1D∩直线A1C=OO∈面BC1DO在面A1C与平面BC1D的交线C1M上∴C1、O、M共线变式训练1:已知空间四点A、B、C、D不在同一平面内,求证:直线AB和CD既不相交也不平行.提示:反证法.例2.已知直线与三条平行线a、b、c都相交.求证:与a、b、c共面.证明:设a∩l=Ab∩l=Bc∩l=Ca∥ba、b确定平面αlβA∈a,B∈b用心爱心专心2典型例题基础过关CODABMB1C1D1A1证明:(1)∵AA1∩BB1=0,∴AA1与BB1确定平面α,又∵A∈a,B∈α,A1∈α,B1∈α,∴ABα,A1B1α,∴AB、A1B1在同一个平面内同理BC、B1C1、AC、A1C1分别在同一个平面内(2)设AB∩A1B1=X,BC∩B1C1=Y,AC∩A1C1=Z,则只需证明X、Y、Z三点都是平面A1B1C1与ABC的公共点即可.变式训练3:如图,在正方体ABCD-A1B1C1D1中,E为AB中点,F为AA1中点,求证:(1)E、C.D1、F四点共面;(2)CE、D1F、DA三线共点.证明(1)连结A1B则EF∥A1BA1B∥D1C∴EF∥D1C∴E、F、D1、C四点共面(2)面D1A∩面CA=DA∴EF∥D1C且EF=D1C∴D1F与CE相交又D1F面D1A,CE面AC∴D1F与CE的交点必在DA上∴CE、D1F、DA三线共点.例4.求证:两两相交且不通过同一点的四条直线必在同一平面内.证明:(1)若a、b、c三线共点P,但点pd,由d和其外一点可确定一个平面α又a∩d=A∴点A∈α∴直线aα同理可证:b、cα∴a、b、c、d共面(2)若a、b、c、d两两相交但不过同一点∵a∩b=Q∴a与b可确定一个平面β又c∩b=E∴E∈β同理c∩a=F∴F∈β∴直线c上有两点E、F在β上∴cβ同理可证:dβ故a、b、c、d共面由(1)(2)知:两两相交而不过同一点的四条直线必共面变式训练4:分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线,为什么?解:假设AC、BD不异面,则它们都在某个平面内,则A、B、C、D.由公理1知,.这与已知AB与CD异面矛盾,所以假设不成立,即AC、BD一定是异面直线。1.证明若干点共线问题,只需证明这些点同在两个相交平面.2.证明点、线共面问题有两种基本方法:①先假定部分点、线确定一个平面,再证余下的点、线在此平面内;②分别用部分点、线确定两个(或多个)平面,再证这些平面重合.3.证明多线共点,只需证明其中两线相交,再证其余的直线也过交点.用心爱心专心OC1B1A1ABC3ABECDFA1B1C1D1小结归纳用心爱心专心4