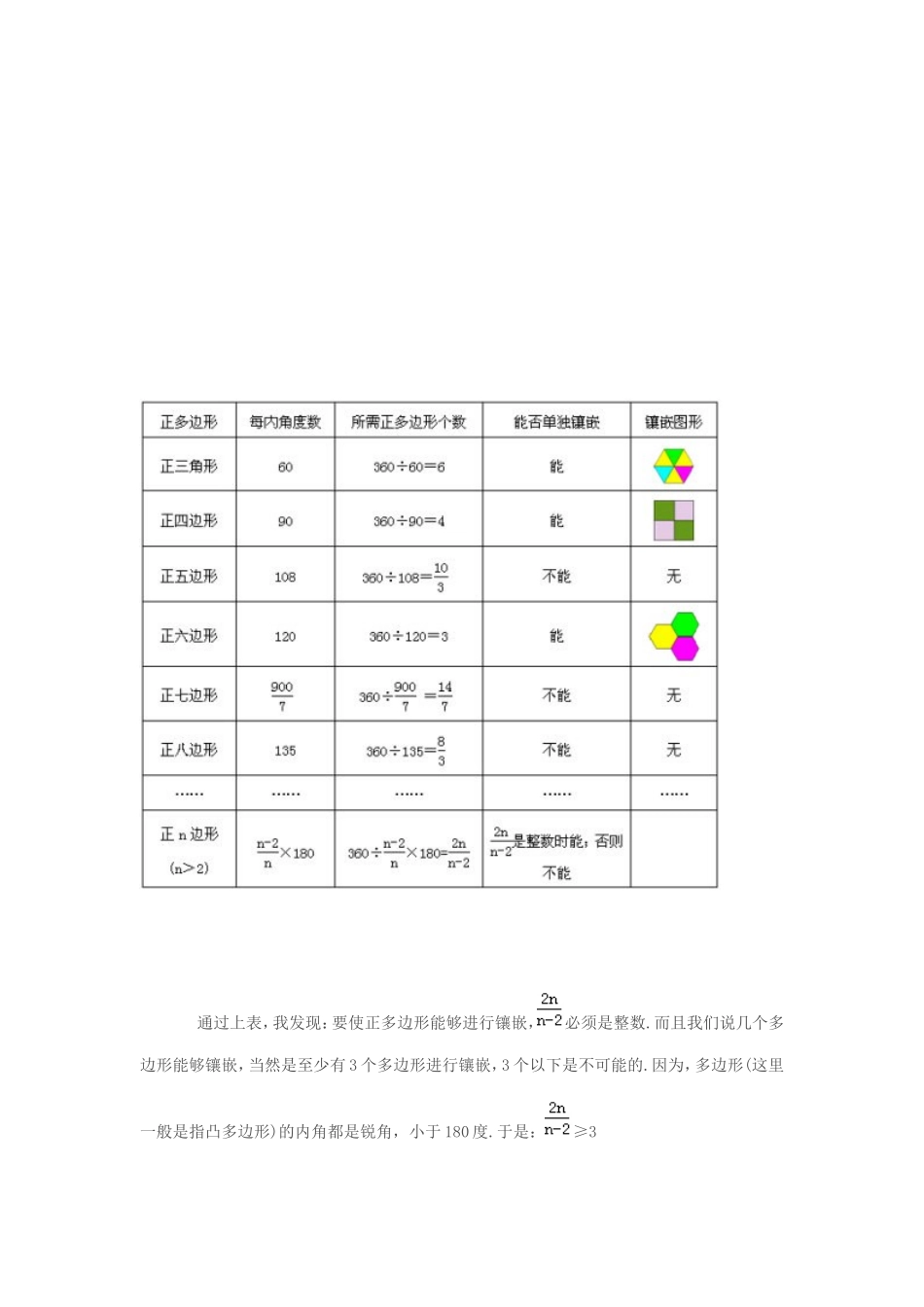
正多边形的镶嵌规律(学生小论文)(2009-04-2722:10:48)转载标签:杂谈分类:学生作品鹿城区临江中学程健力学习了《美妙的镶嵌》,我知道镶嵌的两个基本特征:(1)拼接点处的各个角之和等于360度.(2)拼接边相等.课后老师布置了作业——请同学们设计一个镶嵌图形.这是一个非常好的作业,老师没有规定用什么图形进行镶嵌,可以任意选择图形.于是课堂上老师给我们展示了许多美丽的镶嵌图形,便浮现在我的脑海中.这些镶嵌图形,有的是单一多边形进行镶嵌,也有的几种多边形进行镶嵌;有的是一般多边形进行镶嵌,有的是正多边形进行镶嵌.到底是怎样的正多边形可以进行镶嵌呢?一、探索单种正多边形镶嵌问题.能够镶嵌的条件之一是,拼接点处的几个角的和为360°。用单一正多边形进行镶嵌,就是要求几个正多边形的内角的和为360°.如下表:通过上表,我发现:要使正多边形能够进行镶嵌,必须是整数.而且我们说几个多边形能够镶嵌,当然是至少有3个多边形进行镶嵌,3个以下是不可能的.因为,多边形(这里一般是指凸多边形)的内角都是锐角,小于180度.于是:≥3两边同时乘以n-2( n>2,∴n-2>0)得,2n≥3(n-2)解得,n≤6这样看来,表格中六边形以上的多边形是不可能进行单独镶嵌的,而能够进行单独镶嵌的多边形只有三种:(1)6个正三角形;(2)4个正四边形;(3)3个正六边形.二、探索两种正多边形镶嵌问题.镶嵌的关键是内角的度数,所以对正多边形的内角度数必须要有所了解.为了弄清n取何值时中是整数,我在Excel中输入公式,输出60度到179度之间的正多边形内角度数,结果表示如左表,取其中内角度数是整数的多边形内角度数,结果表示成右表:由表格可知中,当n是3,4,5,6,8,9,10,12,15,18,20,24,30,36,40,45,60,72,90,120,180,360,时,是整数,共22个.在上述的22种正多边形中可以两个组合进行镶嵌,共有以下几种:(1)正三角形与三边以上的正多边形镶嵌.1×60+1×300;→1×60+2×150;→1个正三角形,2个正12边形.(√)2×60+1×240;→2×60+2×120;→2个正三角形,2个正6边形.(√)3×60+1×180;→3×60+2×90;→3个正三角形,2个正4边形.(√)4×60+1×120;→4×60+1×120;→4个正三角形,1个正6边形.(√)5×60+1×30;(小于60度舍去)(2)正四边形与四边以上的正多边形镶嵌.1×90+1×270;→1×90+2×135;→1个正四边形,2个正8边形.(√)2×90+1×180;→2×90+2×90;(等于90度舍去)(3)正五边形与五边以上的正多边形镶嵌.1×108+1×252;→1×108+2×126;→1×108+3×84;(小于108度舍去)2×108+1×144;→2×108+1×144;→2个正五边形,1个正10边形.(√)3×108+1×36;(小于108度舍去)(4)正六边形与六边以上的正多边形镶嵌.1×120+1×240;→1×120+2×120;(等于120度舍去)设六边以上的正多边形的内角是x(x>120),所要镶嵌的图形共有n个(n≥3)则:由120+(n-1)x=360得,n=240/x+1再由n≥3得,240/x+1≥3,解得x≤120显然,对于六边以上的正多边形是无法用2种图形进行镶嵌.因此,两种正多边形进行镶嵌只有六种:(1)1个正三角形,2个正12边形;(2)2个正三角形,2个正6边形;(3)3个正三角形,2个正4边形;(4)4个正三角形,1个正6边形;(5)1个正四边形,2个正8边形;(6)2个正五边形,1个正10边形.三、探索三种正多边形镶嵌问题.根据探索二的结论,可以将探索二中的正多边形分成两个不相同的正多边形,组成三种正多边形的镶嵌.由探索二中的(1)变化出如下:(1)1×60+2×150→1×60+2×90+1×120→1个正三角形,2个正4边形,1个正6边形;(2)1×60+2×150→1×60+1×135+1×165→1个正三角形,1个正8边形,1个正24边形;(3)1×60+2×150→1×60+1×140+1×160→1个正三角形,1个正9边形,1个正18边形;(4)1×60+2×150→1×60+1×144+1×156→1个正三角形,1个正10边形,1个正25边形.由探索二中的(2)变化出如下:(1)2×60+2×120→2×60+1×90+1×150→2个正三角形,1个正4边形,1个正12边形.由探索二中的(3)(4)无法变化.由探索二中的(5)变化如下:(1)1×90+2×135→1×90+1×108+1×162→1个正4边形,1个正4边形,1个正20边形;(2)1×90+2×135→1×90+1×120+1×150→1个正4边形,1个正6边形,1个正...