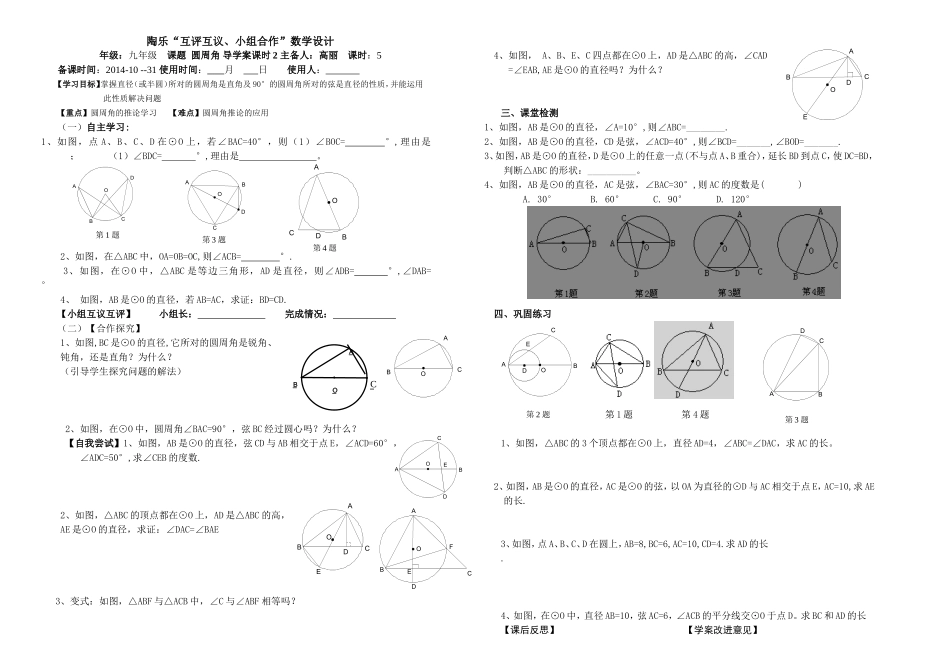
OCBAEODCBAEODCBAFEODCBAABECDO陶乐“互评互议、小组合作”数学设计年级:九年级课题圆周角导学案课时2主备人:高丽课时:5备课时间:2014-10--31使用时间:月日使用人:【学习目标】掌握直径(或半圆)所对的圆周角是直角及90°的圆周角所对的弦是直径的性质,并能运用此性质解决问题【重点】圆周角的推论学习【难点】圆周角推论的应用(一)自主学习:1、如图,点A、B、C、D在⊙O上,若∠BAC=40°,则(1)∠BOC=°,理由是;(1)∠BDC=°,理由是。2、如图,在△ABC中,OA=OB=OC,则∠ACB=°.3、如图,在⊙O中,△ABC是等边三角形,AD是直径,则∠ADB=°,∠DAB=°4、如图,AB是⊙O的直径,若AB=AC,求证:BD=CD.【小组互议互评】小组长:完成情况:(二)【合作探究】1、如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?为什么?(引导学生探究问题的解法)2、如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?【自我尝试】1、如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.2、如图,△ABC的顶点都在⊙O上,AD是△ABC的高,AE是⊙O的直径,求证:∠DAC=∠BAE3、变式:如图,△ABF与△ACB中,∠C与∠ABF相等吗?4、如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=∠EAB,AE是⊙O的直径吗?为什么?三、课堂检测1、如图,AB是⊙O的直径,∠A=10°,则∠ABC=________.2、如图,AB是⊙O的直径,CD是弦,∠ACD=40°,则∠BCD=_______,∠BOD=_______.3、如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,使DC=BD,判断△ABC的形状:__________。4、如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是()A.30°B.60°C.90°D.120°四、巩固练习第1题第4题1、如图,△ABC的3个顶点都在⊙O上,直径AD=4,∠ABC=∠DAC,求AC的长。2、如图,AB是⊙O的直径,AC是⊙O的弦,以OA为直径的⊙D与AC相交于点E,AC=10,求AE的长.3、如图,点A、B、C、D在圆上,AB=8,BC=6,AC=10,CD=4.求AD的长.4、如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点D。求BC和AD的长【课后反思】【学案改进意见】ODCBA第1题ODCBA第3题ODCBA第4题_O_A_B_CCDAB第3题ABCDOE第2题