计量经济学讲义VIP免费

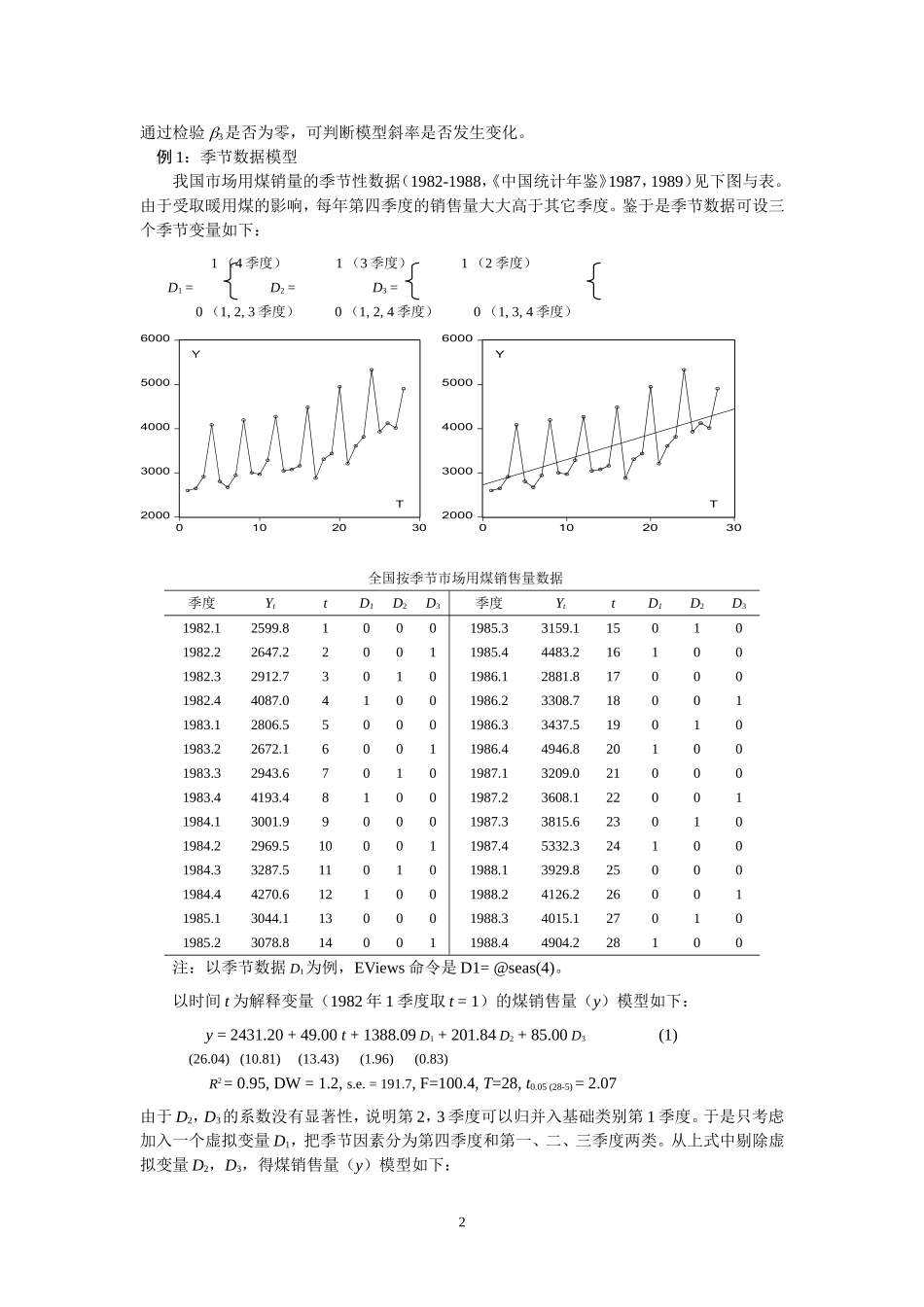
虚拟变量（dummyvariable）在实际建模过程中，被解释变量不但受定量变量影响，同时还受定性变量影响。例如需要考虑性别、民族、不同历史时期、季节差异、企业所有制性质不同等因素的影响。这些因素也应该包括在模型中。由于定性变量通常表示的是某种特征的有和无，所以量化方法可采用取值为1或0。这种变量称作虚拟变量，用D表示。虚拟变量应用于模型中，对其回归系数的估计与检验方法与定量变量相同。1．截距移动设有模型，yt=0+1xt+2D+ut,其中yt，xt为定量变量；D为定性变量。当D=0或1时，上述模型可表达为，0+1xt+ut,(D=0)ytD=1yt=0+2D=0(0+2)+1xt+ut,(D=1)0xtD=1或0表示某种特征的有无。反映在数学上是截距不同的两个函数。若2显著不为零，说明截距不同；若2为零，说明这种分类无显著性差异。例：中国成年人体重y（kg）与身高x（cm）的回归关系如下：–105+xD=1(男)y=-100+x-5D=–100+xD=0(女)注意：①若定性变量含有m个类别，应引入m-1个虚拟变量，否则会导致多重共线性，称作虚拟变量陷阱（dummyvariabletrap）。②关于定性变量中的哪个类别取0，哪个类别取1，是任意的，不影响检验结果。③定性变量中取值为0所对应的类别称作基础类别（basecategory）。④对于多于两个类别的定性变量可采用设一个虚拟变量而对不同类别采取赋值不同的方法处理。如：1(大学)D=0(中学)-1(小学)。2．斜率变化以上只考虑定性变量影响截距，未考虑影响斜率，即回归系数的变化。当需要考虑时，可建立如下模型：yt=0+1xt+2D+3xtD+ut,其中xt为定量变量；D为定性变量。当D=0或1时，上述模型可表达为，(0+2)+(1+3)xt+ut,(D=1)ytD=1yt=0+2D=00+1xt+ut,(D=0)0xt1通过检验3是否为零，可判断模型斜率是否发生变化。例1：季节数据模型我国市场用煤销量的季节性数据（1982-1988，《中国统计年鉴》1987，1989）见下图与表。由于受取暖用煤的影响，每年第四季度的销售量大大高于其它季度。鉴于是季节数据可设三个季节变量如下：1（4季度）1（3季度）1（2季度）D1=D2=D3=0（1,2,3季度）0（1,2,4季度）0（1,3,4季度）200030004000500060000102030TY200030004000500060000102030TY全国按季节市场用煤销售量数据季度YttD1D2D3季度YttD1D2D31982.12599.810001985.33159.1150101982.22647.220011985.44483.2161001982.32912.730101986.12881.8170001982.44087.041001986.23308.7180011983.12806.550001986.33437.5190101983.22672.160011986.44946.8201001983.32943.670101987.13209.0210001983.44193.481001987.23608.1220011984.13001.990001987.33815.6230101984.22969.5100011987.45332.3241001984.33287.5110101988.13929.8250001984.44270.6121001988.24126.2260011985.13044.1130001988.34015.1270101985.23078.8140011988.44904.228100注：以季节数据D1为例，EViews命令是D1=@seas(4)。以时间t为解释变量（1982年1季度取t=1）的煤销售量（y）模型如下：y=2431.20+49.00t+1388.09D1+201.84D2+85.00D3(1)(26.04)(10.81)(13.43)(1.96)(0.83)R2=0.95,DW=1.2,s.e.=191.7,F=100.4,T=28,t0.05(28-5)=2.07由于D2，D3的系数没有显著性，说明第2，3季度可以归并入基础类别第1季度。于是只考虑加入一个虚拟变量D1，把季节因素分为第四季度和第一、二、三季度两类。从上式中剔除虚拟变量D2，D3，得煤销售量（y）模型如下：2y=2515.86+49.73t+1290.91D1(2)(32.03(10.63)(14.79)R2=.94,DW=1.4,s.e.=198.7,F=184.9,T=28,t0.05(25)=2.06进一步检验斜率是否有变化，在上式中加入变量tD1，y=2509.07+50.22t+1321.19D1-1.95tD1(3)(28.24)(9.13)(6.85)(-0.17)R2=.94,DW=1.4,s.e.=202.8,F=118.5,T=28,t0.05(24)=2.06由于回归系数-1.95所对应的t值是-0.17，可见斜率未发生变化。因此以模型(2)作为最后确立的模型。若不采用虚拟变量，得回归结果如下，y=2731.03+57.15t(4)(11.6)(4.0)R2=0.38,DW=2.5,s.e.=608.8,T=28,t0.05(26)=2.06与（2）式相比，回归式（4）显得很差。例2：用虚拟变量区别不同历史时期中国进出口贸易总额数据（1950-1984）见上表。试检验改革前后该时间序列...