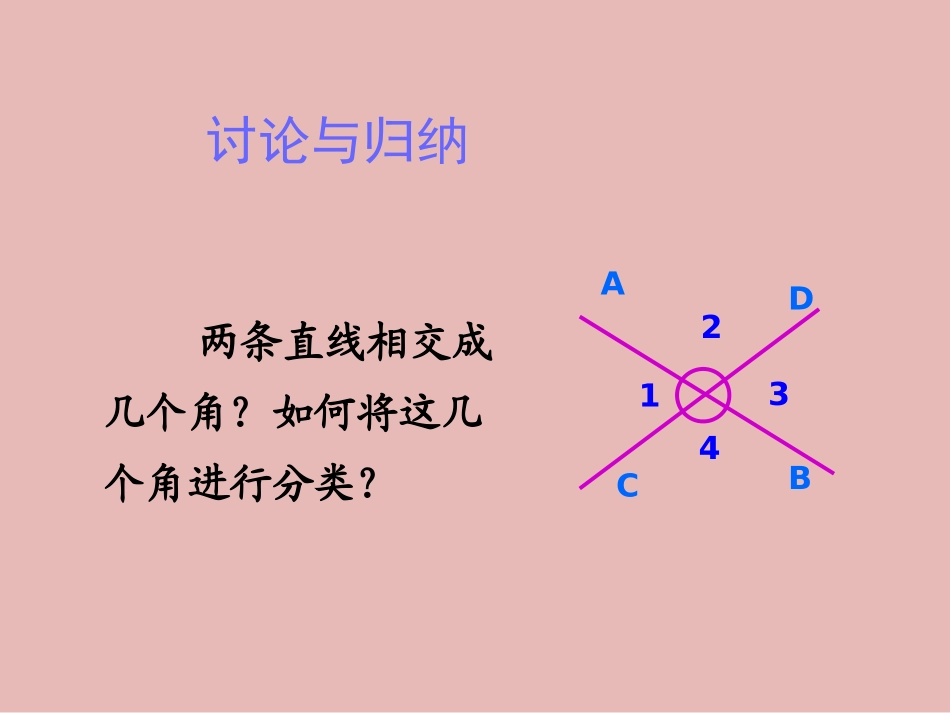
5.1相交线第五章相交线与平行线5.1.1相交线复习与回顾2、什么叫相交直线?当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。1、点与直线有什么位置关系?⑴点在直线上;⑵点在直线外;ABOabABCD1234讨论与归纳两条直线相交成几个角?如何将这几个角进行分类?∠1与∠3是两条直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角。∠2与∠4也是对顶角,共有两对。对顶角的概念ABCD1234∠1和∠2也是两条直线AB、CD相交得到的,它们不仅有一个公共顶点O,还有一条公共边OA,像这样的两个角叫做邻补角.图中的邻补角还有∠2与∠3、∠3与∠4、∠4与∠1,共有四对。邻补角性质:邻补角互补(两个角的和是180°)ABCD1234练习:下列各图中,∠1和∠2是对顶角吗?121212练习:图中∠1和∠2是邻补角吗?21图中∠1与∠2互为补角,但不是邻补角相同:两个角的和是180°不同:位置关系不同练习:找出图中的对顶角。ABCDEFOABCDEO辨认对顶角的要领:前提条件——两条直线相交;找其中有公共定点没有公共边(或不相邻)的两个角ABCD1234对顶角的性质∵∠1与∠2互补∠3与∠2互补(邻补角定义)(邻补角定义)∴∠1=∠3(同角的补角相等)对顶角的性质:对顶角相等解:∵∠3=∠1=40°(对顶角相等)∠2=180°-40°=140°(邻补角定义)∴∠4=∠2=140°(对顶角相等)已知:直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数。1234ab例题讲解变式训练变式1:把∠1=40°变为∠1=90°变式2:把∠1=40°变为∠2是∠1的3倍变式3:把∠1=40°变为∠1∶∠2=2∶7变式4:把∠1=40°变为?1234ab已知:直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数。1、若∠α与∠β是对顶角,∠α=16°则∠β=。2、如图,三条直线a、b、c相交于点O,∠1=40°∠2=75°则∠3=。3、如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD=,∠BOC=。ABCDEOabc123练习:填空4、两条直线相交得四个角,其中一个角是90°其余各角是。5、已知直线AB、CD相交于点O,∠AOC=28°,OE平分∠AOD,求∠EOB的度数。ABCDEO归纳小结①两条直线相交形成的角②有一个公共顶点;③没有公共边①两条直线相交而成;②有一个公共点;③有一条公共边对顶角相等角的名称特征性质相同点不同点对顶角邻补角邻补角互补①都是两条直线相交而成的角;②都有一个公共顶点;③都是成对出现的①有无公共边②两直线相交时,对顶角有两对,而邻补角有四对1.若∠2是∠1的3倍,求∠3的度数?ab12342.若∠2-∠1=400,求∠4的度数?作业:书面作业:A:P8—2;P9—7B:P8—2;P9—7;P10—13“1+1”:A:B:两条直线相交垂线对顶角:相等邻补角:互补垂线的存在性和唯一性特殊情况相交成直角一般情况5.1.3同位角、内错角、同旁内角例1如图,两条直线AB、CD都与第三条直线EF相交.(1)构成几个小于平角的角?8个EFABCD67581234∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8.(2)同位角有哪些?EFABCD67581234∠3与∠5,∠4与∠6.(3)内错角有哪些?EFABCD6534∠3与∠6,∠4与∠5.(4)同旁内角有哪些?EFABCD6534例2如图,找出图中所有的同位角、内错角、同旁内角.1234ABCDEF∠1与∠3,∠2与∠4.同位角:1234ABCDEF没有.内错角:1234ABCDEF∠2与∠3.同旁内角:1234ABCDEFBACED324511.(1)如图,1∠与是内错角,是直线和被直线___所截而成的角;∠3BCDEAB(2)2∠与∠4是直线和被直线所截而成的角;BCDEACBACED32451内错(3)2∠与∠DAC是直线和被直线所截成的角.DEBCAC同旁内BACED324512.如图,直线DE、BC被直线AB所截.ABDCE2431(1)1∠与∠2,∠1与∠3,∠1与∠4是什么角?∠1与∠2是内错角,∠1与∠3是同旁内角,∠1与∠4是同位角.(2)如果∠1=4∠,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?ABDCE2431∠1和∠2相等,∠1和∠3互补.3.如图,找出图中数字标注的角的同位角,内错角,同旁内角.1234561236同位角:2346内错角:1245内错角:1346同旁内角:1234同旁内角:1345同旁内角:由“三线八角”图形判断同位角,内错角,同旁内角或由同位角,内错角,同旁内角找出构成它们的“三线”,都要有一个步骤:一看角的顶点,二看角的边,三看角的方位,这三看又离不开主线——截线的确定.