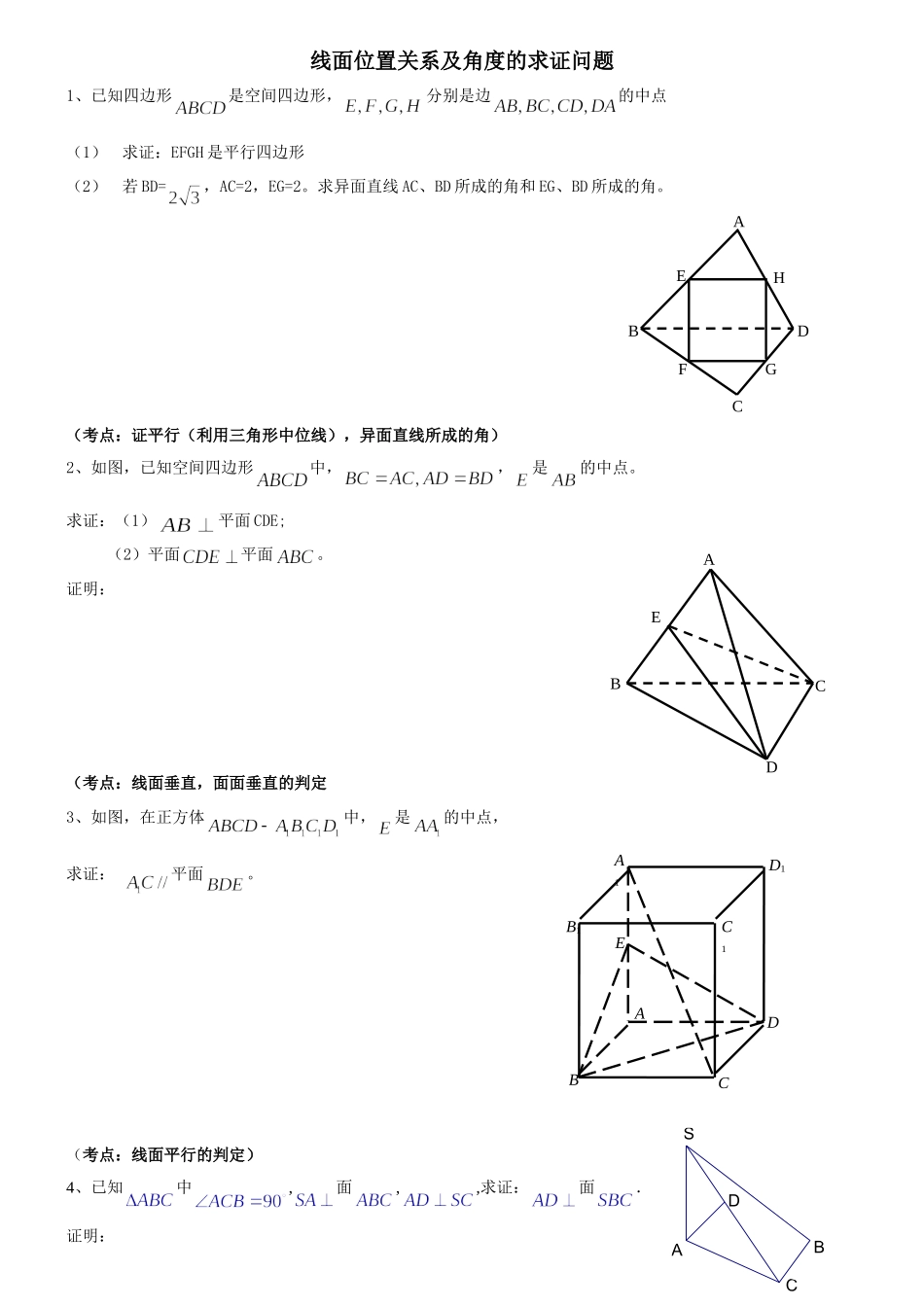
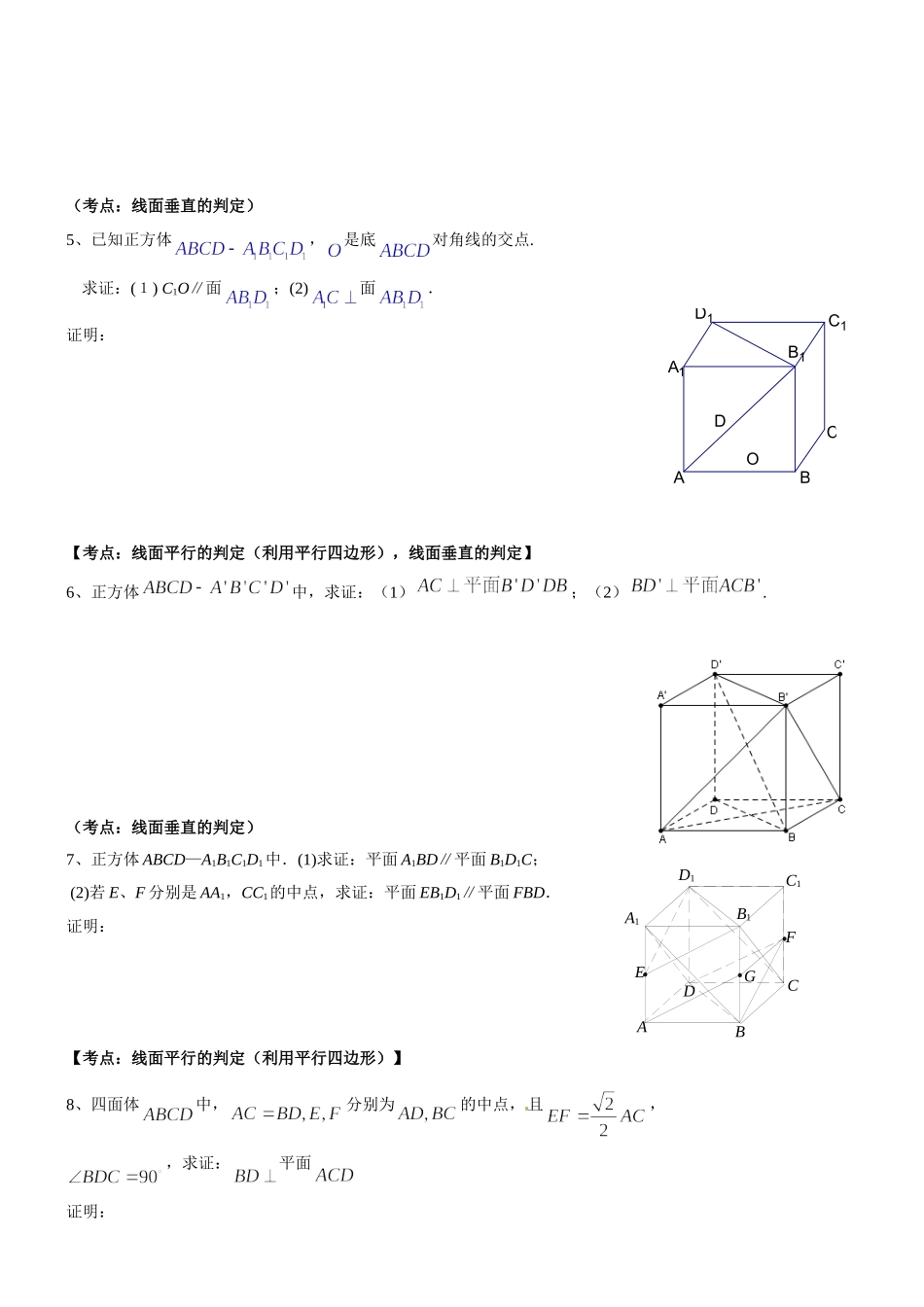
线面位置关系及角度的求证问题1、已知四边形是空间四边形,分别是边的中点(1)求证:EFGH是平行四边形(2)若BD=,AC=2,EG=2。求异面直线AC、BD所成的角和EG、BD所成的角。(考点:证平行(利用三角形中位线),异面直线所成的角)2、如图,已知空间四边形中,,是的中点。求证:(1)平面CDE;(2)平面平面。证明:(考点:线面垂直,面面垂直的判定3、如图,在正方体中,是的中点,求证:平面。(考点:线面平行的判定)4、已知中,面,,求证:面.证明:A1ED1C1B1DCBAAHGFEDCBAEDBCSDCBA(考点:线面垂直的判定)5、已知正方体,是底对角线的交点.求证:(1)C1O∥面;(2)面.证明:【考点:线面平行的判定(利用平行四边形),线面垂直的判定】6、正方体中,求证:(1);(2).(考点:线面垂直的判定)7、正方体ABCD—A1B1C1D1中.(1)求证:平面A1BD∥平面B1D1C;(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.证明:【考点:线面平行的判定(利用平行四边形)】8、四面体中,分别为的中点,且,,求证:平面证明:D1ODBAC1B1A1CA1AB1BC1CD1DGEFNMPCBA【考点:线面垂直的判定,三角形中位线,构造直角三角形】9、如图是所在平面外一点,平面,是的中点,是上的点,(1)求证:;(2)当,时,求的长。证明:(考点:三垂线定理)10、如图,在正方体中,、、分别是、、的中点.求证:平面∥平面.证明:【考点:线面平行的判定(利用三角形中位线)】11、如图,在正方体中,是的中点.(1)求证:平面;(2)求证:平面平面.证明:【考点:线面平行的判定(利用三角形中位线),面面垂直的判定】12、已知是矩形,平面,,,为的中点.(1)求证:平面;(2)求直线与平面所成的角.证明:(考点:线面垂直的判定,构造直角三角形)13、如图,在四棱锥中,底面是且边长为的菱形,侧面是等边三角形,且平面垂直于底面.(1)若为的中点,求证:平面;(2)求证:;(3)求二面角的大小.证明:【考点:线面垂直的判定,构造直角三角形,面面垂直的性质定理,二面角的求法(定义法)】14、如图1,在正方体中,为的中点,AC交BD于点O,求证:平面MBD.证明:【考点:线面垂直的判定,运用勾股定理寻求线线垂直】15、如图2,在三棱锥A-BCD中,BC=AC,AD=BD,作BE⊥CD,E为垂足,作AH⊥BE于H.求证:AH⊥平面BCD.证明:(考点:线面垂直的判定)16、证明:在正方体ABCD-A1B1C1D1中,A1C⊥平面BC1DD1C1A1B1DCAB(考点:线面垂直的判定,三垂线定理)17、如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.证明:【考点:面面垂直的判定(证二面角是直二面角)】