2012年温州中学自主招生数学试题 VIP免费

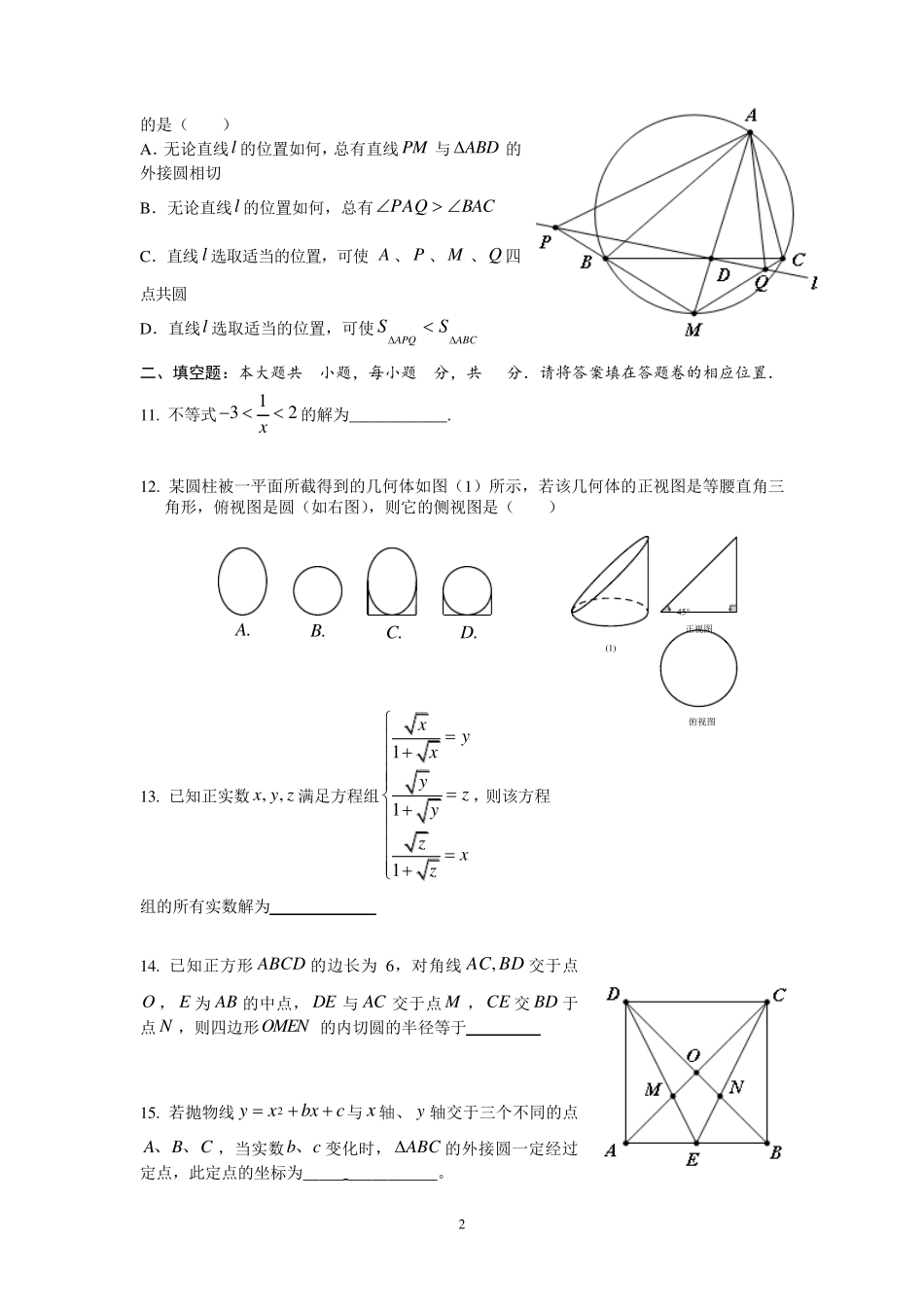
1温州中学自主招生数学试题（本试卷满分150分，考试时间120分钟）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的的四个选项中，只有一项是符合题目要求的．请将你认为正确的答案填在答题卷的相应位置．1.使xzzyyx,,都有意义的实数组,,xyz（）A．存在且有无限多组B．存在有限组C．一定不存在D．无法确定是否存在2.如图所示，直线1l，2l，3l表示三条相交的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有A．1处B．2处C．3处D．4处3.下列函数中和函数11yx的图像关于y轴对称的（）A.11yxB.11yxC.11yxD.11yx4.小明、小联、小豪人一起玩“剪刀、石头、布”的游戏。每一局三人同时出“剪刀、石头、布”中的一种手势。则小明只赢一人的概率为（）A.29B.49C.227D.4275.若030，则sin,cos,tan,的大小关系是（）A.sincostanB.sintancosC.tansincosD.tancossin6.三角形三条高线之比为20:15:12，则这三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．形状不能确定7.对于满足2x的所有实数x，使不等式212ppxpx恒成立，则p的取值范围为（）A．1pB．1p或1pC．3p或1pD．3p或1p8.定义函数[[]]yxx，其中[]x表示不超过x的最大整数，如：1.51,1.32。当)(,0*Nnnx时，记na为函数y的所有可能取值的个数。则10a（）A．45B．46C．55D．669.十进制中，四位数能满足下列条件的就叫做“和谐平方数”：（1）它的数字都不为零；（2）它是一个完全平方数；（3）这个数的前两位数字，后两位数字都是完全平方数（看做两位数时）问这样的“和谐平方数”的个数为（）A.1B.2C.3D.410.如图，已知A的平分线分别与边BC、ABC的外接圆交于点D、M，过D任作一条与直线BC不重合的直线l，直线l分别与直线MB、MC交于点P、Q，下列判断错误．．l2l1l32的是（）A．无论直线l的位置如何，总有直线PM与ABD的外接圆相切B．无论直线l的位置如何，总有PAQBACC．直线l选取适当的位置，可使A、P、M、Q四点共圆D．直线l选取适当的位置，可使ABCAPQSS二、填空题：本大题共6小题，每小题5分，共30分．请将答案填在答题卷的相应位置．11.不等式132x的解为____________.12.某圆柱被一平面所截得到的几何体如图（1）所示，若该几何体的正视图是等腰直角三角形，俯视图是圆（如右图），则它的侧视图是（）13.已知正实数,,xyz满足方程组111xyxyzyzxz，则该方程组的所有实数解为14.已知正方形ABCD的边长为6，对角线BDAC,交于点O，E为AB的中点，DE与AC交于点M，CE交BD于点N，则四边形OMEN的内切圆的半径等于15.若抛物线2yxbxc与x轴、y轴交于三个不同的点ABC、、，当实数bc、变化时，ABC的外接圆一定经过定点，此定点的坐标为________________。(1)正视图俯视图45°D.C.B.A.316.我们把2×2的方格表称为一个“宫”，如图所示，将4个“宫”拼成一个4×4的方格表（称为“四宫格”）。现将1,2,3,4四个数字填入“四宫格”中，使得这4个数字在每行、每列、每“宫”（共4个）的四个格子中均出现一次。现已知四宫格左上角的方格内已经填有数字1，则满足条件的填法共有种。三、解答题：本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．17.（本题满分10分）已知1x，1y，求证：111xyxyxyxy18.（本题满分14分）如图，已知双曲线11:Cyx、抛物线22:12Cyx，直线:lykxm.（Ⅰ）若直线l与抛物线2C有公共点，求24km的最小值；（Ⅱ）设直线l与双曲线1C的两个交点为AB、，与抛物线2C的两个交点为CD、.是否存在直线l，使得AB、为线段CD的三等分点？若存在，求出直线l的解析式，若不存在，请说明理由。1419.（本题满分16分）现有一方格盘的跳棋，即在一个无限大的方格棋盘上有若干枚棋子，规定每一步可将某枚棋子跳过邻格中的棋子而进入随后的空格中，同时将被其他棋子跳过的棋子从棋盘上拿走。（1）当棋盘上最初只有摆放成“7”字型的4枚棋子时，最终最...