二次函数的图像与性质(6)VIP免费

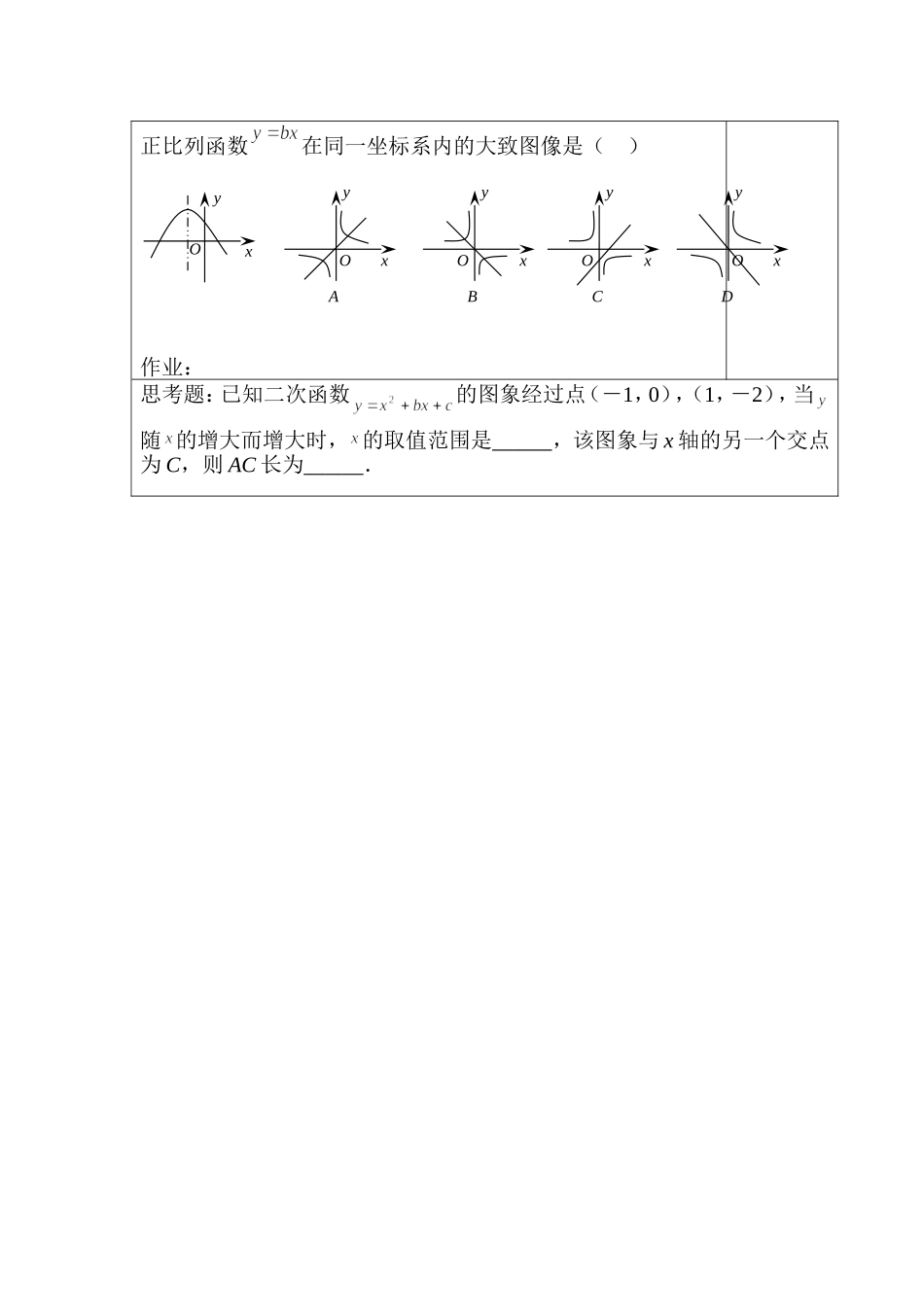
九年级下册数学学案班级姓名课题二次函数图像与性质（6）课型新授+展示课学习目标1、掌握二次函数的一般式的性质。2、掌握利用二次函数的一般式的性质来解决函数的问题。重点二次函数的一般式的性质难点能熟练利用二次函数的一般式的性质来解决实际问题。一、学习回顾：1、将函数配方成顶点式为：y=，说出二次函数一般式的性质。2、填写下表：二、教师精讲：1、若抛物线y=21x2+bx－2过A（一1，0）．⑴求抛物线的解析式；（2）写出抛物线的对称轴顶点的坐标，并说出函数的最值。变式训练：.1、已知二次函数y=ax2＋bx－3的图象经过点A（2，－3），B（－1，0）．求二次函数的解析式学习笔记二次函数开口方向对称轴顶点坐标O第20题yAxCB三、合作探究：巩固训练1：1、二次函数522xxy有（）A．最大值5B．最小值5C．最大值6D．最小值62、抛物线y=x2-2x-3的顶点坐标是.3、二次函数2365yxx的图像的顶点坐标是（）A．（-1，8）B．（1，8）C．（-1，2）D．（1，-4）4、如图，已知二次函数cbxxy2的图象经过点（－1，0），（1，－2），当y随x的增大而增大时，x的取值范围是．巩固训练2：5、．如图，已知二次函数y＝—x2＋bx＋c的图象经过A（2，0）、B（0，—6）两点．（1）求这个二次函数的解析式；（2）求函数的的最值。（2）设该二次函数图象的对称轴与x轴交于点C，连结BA、BC，求△ABC的面积．课堂检测：1.（2010年金华）已知抛物线的开口向下,顶点坐标为（2，－3）,那么该抛物线有（）A.最小值－3B.最大值－3C.最小值2D.最大2、将二次函数y=x22x3化为y=(xh)2k的形式，结果为（）(A)y=(x1)24(B)y=(x1)24(C)y=(x1)22(D)y=(x1)22。3、二次函数的图像如图所示，反比列函数与学习笔记xyO11（1,-2）cbxxy2-1正比列函数在同一坐标系内的大致图像是（）作业：思考题：已知二次函数的图象经过点（－1，0），（1，－2），当随的增大而增大时，的取值范围是，该图象与x轴的另一个交点为C，则AC长为．OxyOyxAOyxBOyxDOyxC