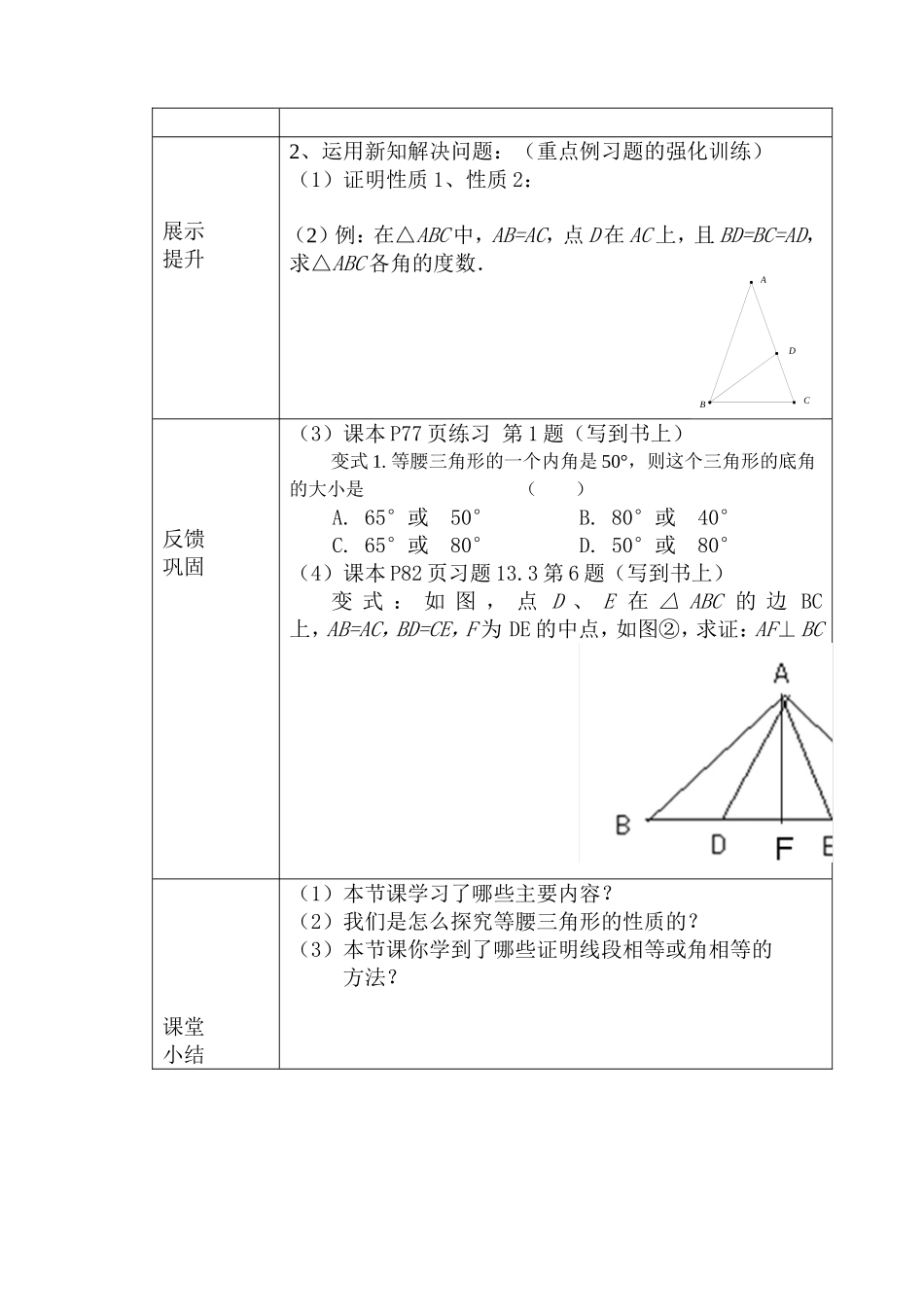
$13.3.1等腰三角形(一)教学设计知识要点等腰三角形的性质教学内容教材第75-77页学习目标1、理解等腰三角形的概念.2、掌握等腰三角形的性质.3、学会等腰三角形的概念及性质的应用.4、经历作(画)出等腰三角形的过程,从轴对称的角度去体会等腰三角形的特点.5、在探究等腰三角形性质的过程中培养学生认真思考的习惯.学习重点等腰三角形的概念、性质及应用学习难点等腰三角形三线合一的性质的理解及其应用学具使用多媒体课件、彩纸、小剪刀、三角板等教学环节学习活动自主学习一、探索并证明等腰三角形的性质1.图片引入:图中有些你熟悉的图形吗?它们有什么共同特点?2.实验探究:(1).把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点(1)等腰三角形是不是特殊的三角形?它是否具备三角形所有的性质,比如┅┅(2)等腰三角形是不是轴对称图形?(3)你能独立概括一下等腰三角形的定义吗?试一试。如图,在△ABC中,AB=AC,标出各部分名称等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.(2).剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.合作探究把活动中剪出的△ABC沿折痕AD对折,找出其中重合的线段和角,填入下表重合的线段重合的角归纳总结巩固新知1、知识点的归纳总结:性质1:等腰三角形的两个相等(简写成“”)(1).根据结论画出图形,写出已知和求证.(2).结合所画的图形,你认为证明两个底角相等的思路是什么?(3).如何在一个等腰三角形中构造出两个全等三角形呢?从剪图、折纸的过程中你能获得什么启发?你有几种证明方法?性质2:等腰三角形、、互相重合。(简写成“”)可以分解为三个命题。填一填:根据等腰三角形性质定理2完成下列填空.(1)∵AD是BC边上的高,∴∠_____=∠_____,____=____.(2)∵AD是中线,∴____⊥____,∠_____=∠_____.(3)∵AD是角平分线,∴____⊥____,_____=_____.展示提升2、运用新知解决问题:(重点例习题的强化训练)(1)证明性质1、性质2:(2)例:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.反馈巩固(3)课本P77页练习第1题(写到书上)变式1.等腰三角形的一个内角是50°,则这个三角形的底角的大小是()A.65°或50°B.80°或40°C.65°或80°D.50°或80°(4)课本P82页习题13.3第6题(写到书上)变式:如图,点D、E在△ABC的边BC上,AB=AC,BD=CE,F为DE的中点,如图②,求证:AF⊥BC课堂小结(1)本节课学习了哪些主要内容?(2)我们是怎么探究等腰三角形的性质的?(3)本节课你学到了哪些证明线段相等或角相等的方法?DCBA课后作业教科书习题13.3第1、2、4题.