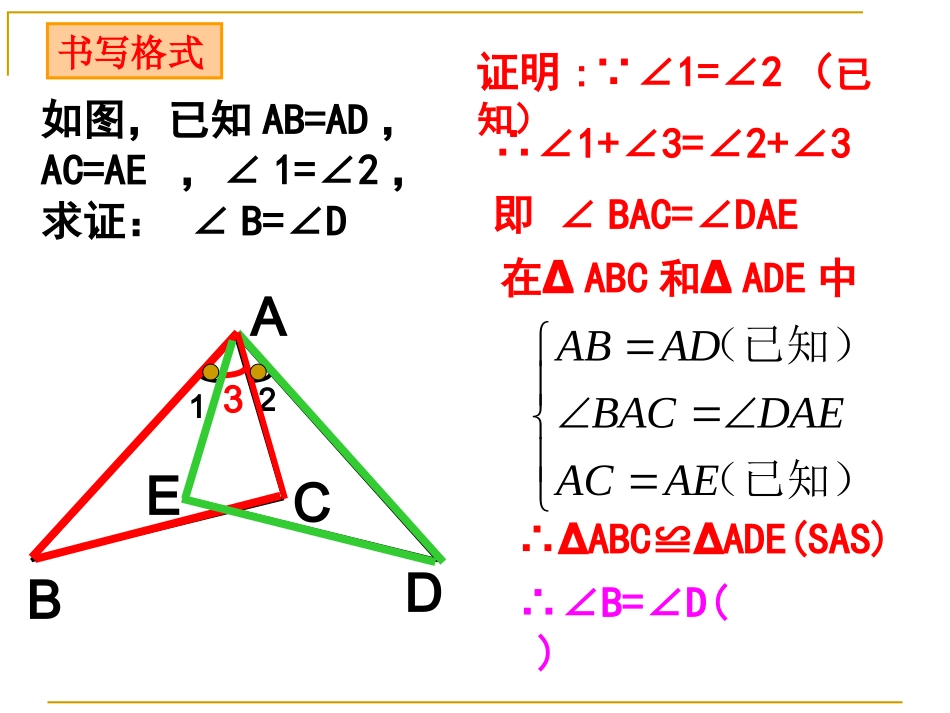
判定条件全等三角形的定义SSSSAS?边和角分别对应相等,而不是分别相等.两个三角形全等特别注意:关键:找符合要求的条件温故知新!知识回顾三角形全等的判定:有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)两边及其夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”)如图,已知AB=AD,AC=AE,∠1=∠2,求证:∠B=∠DABCDE12证明:∵∠1=∠2(已知)∴∠1+∠3=∠2+∠3即∠BAC=∠DAE在∆ABC和∆ADE中∴∆ABC≌ADE(SAS)∆∴∠B=∠D()ABADBACDAEACAE(已知)(已知)书写格式31.5三角形全等的判定(3)如图,小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?所带的这块玻璃里有几个条件已知?想一想:(1)(2)有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?请用量角器和刻度尺画ΔABC,使BC=3,∠B=400、∠C=600将你画的三角形与其他同学画的三角形比较,你发现了什么?CBA6004003cm与同伴进行比较,它们能否互相重合吗?合作学习:ABCA/B/C/∴ΔABC≌ΔA´B´C´(ASA)在△ABC和△A´B´C´中∠B=∠B´BC=B´C´∠C=∠C´有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”)数学语言表示:如图,O是AB的中点,=,与全等吗?为什么?ABAOCBODOABCDBABOAOBODAOCBODAOC)(ASABODAOC和(已知)(中点的定义)(对顶角相等)解:在中≌试着写写看!例4已知:如图,∠1=2∠,∠C=E∠,AC=AE,求证:△ABCADE≌△.解:∵∠1=∠2∴∠1+∠BAE=∠2+∠BAE即∠BAC=∠DAE在△ABC和△ADE中ECAEACDAEBAC===∴△ABCADE(ASA)≌△ACBED12例5已知:如图,点B,F,E,C在同一条直线上,ABCD∥,AB=CD,∠A=∠D.求证:AE=DF.证明:∵ABCD∥∴∠B=∠C在△ABE与△DCF中∠A=∠DAB=DC(公共边)∠B=∠C(已证)∴△ABEDCF≌△(ASA)∴AE=DFACBEDF已知和中,=,AB=AC.ABEACDBC求证:ABCEDOBE=CD;BD=CE.证明:,中和在ACDABECBACABAAACDABE)(ASAAE=AD;ADAE(全等三角形对应边相等)CDBEAEACADABCEBD(已知)(已知)(公共角)(全等三角形对应边相等)(等式的性质)△ABEACD≌△练习.如图,有一湖的湖岸在A,B之间呈一段圆弧状,A,B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?AB——办法总比困难多!皮尺ABOCD2.如图,有一湖的湖岸在A,B之间呈一段圆弧状,A,B间的距离不能直接测得.你能用已学过的知识或方法设计测量方案,求出A,B间的距离吗?提高题:如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作AE的垂线CF,垂足为F,过B作BDBC⊥交CF的延长线于点D.(1)试说明:AE=CD;(2)AC=12cm,求BD的长.解:(1)∵AFDCAFC=90⊥∴∠0又∵∠ACB=90°,∴∠DCB+DCA=EAC+ACF=90°∠∠∠∴∠EAC=DCB∠(同角的余角相等)∵DBBC⊥∴∠DBC=ACB=90∠0∴△DCBEAC≌△(ASA)∴AE=CD在△ACB和△CBD中∠DBC=ACB∠∠EAC=DCB∠AC=BC(2)由(1)得△DCBEAC≌△∴CE=DB∵E为BC的中点∴cmACBCDB62121(1)(1)两角和它们的夹边对应相等的两个三角形全等两角和它们的夹边对应相等的两个三角形全等..简写成“简写成“角边角角边角”或“”或“ASAASA”.”.知识要点:知识要点:((22)探索三角形全等是证明线段相等(对应边相)探索三角形全等是证明线段相等(对应边相等),角相等(对应角相等)等问题的基本途径等),角相等(对应角相等)等问题的基本途径..数学思想:数学思想:要学会用分类的思想,转化的思想解决问题要学会用分类的思想,转化的思想解决问题..ABCDEA1B1C1CDE如图1,已知AB⊥BD,ED⊥BD,AB=CD,BC=DE(1)请说明△ABC≌△CDE,并判断AC是否垂直CE?图1图2拓展提高:(2)若将△ABC沿BC方向平移至如图2的位置时,且其余条件不变,则A1C1是否垂直CE?请说明为什么?