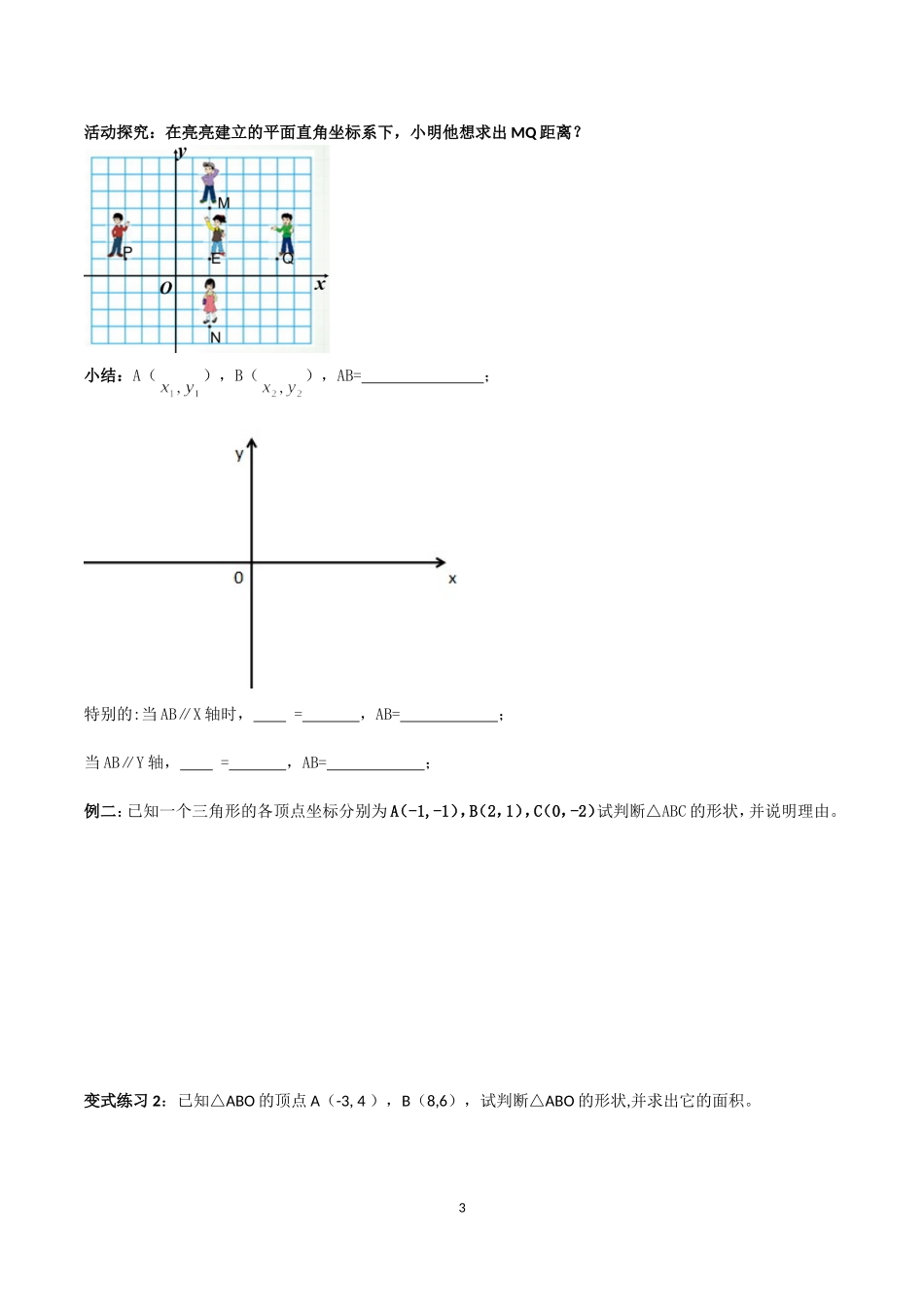
§3.2.2平面直角坐标系学案一、温故:平面直角坐标系中,点P(a,b)的意义:1、点P(a,b)到x轴的距离为;;点P(a,b)到y轴的距离为;2、四个象限,原点,两轴上的点的特点。①P点在X轴上,则b=;②P点在Y轴上,则a=;③PQ∥X轴,则b=;④PQ∥Y轴,则a=;二、知新:【探究1】、有五个小朋友在操场上玩传球游戏,如图是他们位置。萌萌建立直角坐标系后,你最容易说出哪两位之间的距离?小结1:如何求平面直角坐标系中,任意两点之间的距离?若A(x1,y1),B(x2,y2),则AB=①当y1=y2=0,AB在X轴上,AB=②当x1=x2=0,AB在Y轴上,AB=【探究2】在同样的情境下,亮亮建立直角坐标系后,他们中每两个人之间的距离会改变吗?你最容易说出哪些点之间的距离呢?1小结:如何求平面直角坐标系中,任意两点之间的距离?若A(x1,y1),B(x2,y2),则AB=?①当y1=y2,AB∥X轴,AB=②当x1=x2,AB∥Y轴,AB=A(x1,y),B(x2,y),AB=;A(x,y1),B(x,y2),AB=;三、典例精析:例一:已知点A(4,y),B(x,3),若AB∥X轴,且线段AB的长为5,求x,y的值。变式练习1:已知线段AB=7,AB∥Y轴,且A点坐标为(1,2),则点B的坐标为2活动探究:在亮亮建立的平面直角坐标系下,小明他想求出MQ距离?小结:A(),B(),AB=;特别的:当AB∥X轴时,=,AB=;当AB∥Y轴,=,AB=;例二:已知一个三角形的各顶点坐标分别为A(-1,-1),B(2,1),C(0,-2)试判断△ABC的形状,并说明理由。变式练习2:已知△ABO的顶点A(-3,4),B(8,6),试判断△ABO的形状,并求出它的面积。3思考题:如图所示,在平面直角坐标系中,△ABC满足∠ACB=90,AC=4,BC=2,点A,C分别在x,y轴上,当点A从原点开始在X轴正半轴上运动时,点C随着在Y轴上运动。(1)当点A在原点时,求原点O到点B的距离OB。(2)当OA=OC时,求原点O到点B的距离OB。1题图四、本课小结:1、本节课你学到了哪些知识?2、用到了哪些数学思想方法?4