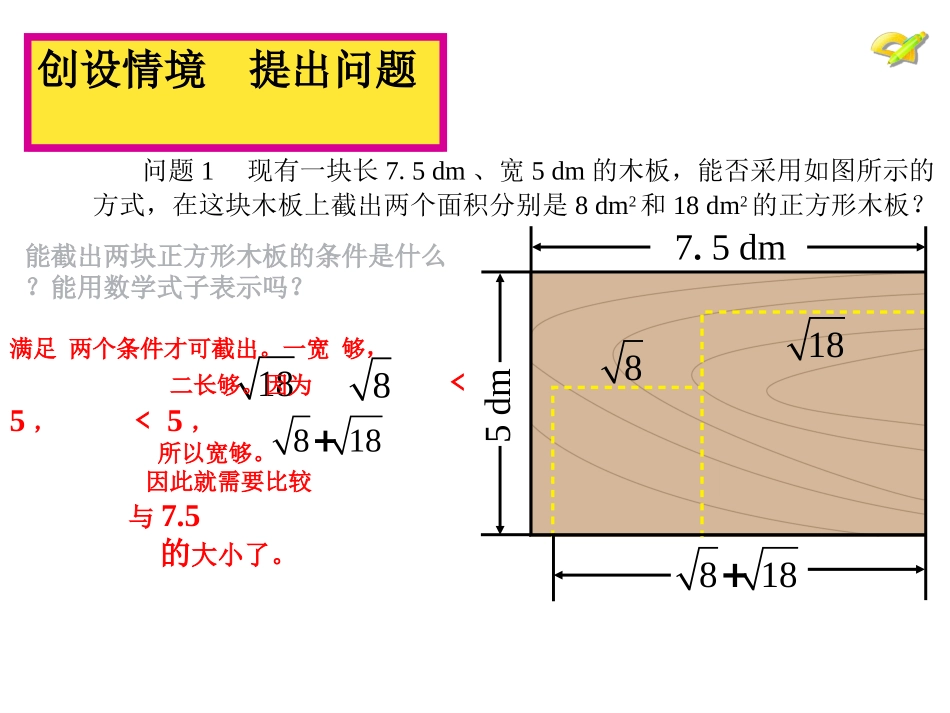
16.3二次根式的加减(1)()2=a(a≥0),=a(a≥0).=(a≥0b≥0),=(a≥0,b>0)a2aabababab温故知新1、复习同学们记得非常牢,但不要忘了公式的逆向应用。问题1现有一块长7.5dm、宽5dm的木板,能否采用如图所示的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?创设情境提出问题能截出两块正方形木板的条件是什么?能用数学式子表示吗?5dm7.5dm188818+188818+满足两个条件才可截出。一宽够,二长够。因为﹤5,﹤5,所以宽够。因此就需要比较与7.5的大小了。创设情境提出问题818+能否进一步计算?这是一种什么运算?5dm7.5dm188818+我看到这是两个二次根式的加法。咱们今天就来解决这个问题。今天咱们就学习二次根式的加减。不过你们可要认真听才会吆。合作探究形成知识818+问题2怎样计算?如果看不出能否化简,我们不妨把问题简化,先看算式能否化简.818+322-322-这里的两个二次根式有什么特征?你能得到这样的两个二次根式加减的方法吗?化简后被开方数相同,即为同类二次根式.二次根式的加减实质上就是将同类二次根式逆用分配律合并.用分配律合并整式加减3--=3--1=(3—1)=2二次根式的性质××合作探究形成知识1、算式与算式有什么相同点与不同?818+322-818223223252+=+=+=()2、现在你会化简算式,并说出每一步化简的理由.818+化为最简二次根式用分配律合并整式加减1、相同点:都是二次根式的加减;不同点:一个不是最简的二次根式加减,一个是最简的二次根式加减。二次根式性质分配律整式加减法则2、合作探究形成知识.1、现在能解决本课开始时提出的问题了吗?+=2+3=(2+3)=5解:5﹤5x1.5=7.5所以长也够,能截出两个这样的正方形2、根据所学内容,请同学们发挥一下你的归纳总结能力,总结一下二次根式加减的步骤、做题每一步的依据、及解决问题基本思想。合作探究形成知识步骤:一化:把不是最简二次根式化成最简二次根式。二找:找化简后的二次根式是否为同类二次根式三合并:合并同类二次根式。依据:二次根式的性质、分配律和整式加减法则;基本思想:把二次根式加减问题转化为整式加减问题.请总结二次根式加减的步骤、依据和基本思想.初步应用巩固知识初步应用巩固知识例1计算:8045(1).8045解:(1)45355aa259)2(aa259)2(aa53a8初步应用巩固知识初步应用巩固知识练习1计算:12126+3483(1)(1220)+(3-5)(2).32236+343343-23+123解:12126+3483(1)143一定要细心!化简要彻底!初步应用巩固知识初步应用巩固知识例2计算:12126+3483(1)(1220)+(3-5)(2).解:(1220)+(3-5)(2)2325+3-533+5化简、去括号、合并请同学们看大屏幕,注意例2的书写过程。所有的同类型一定要合并完。答案:(1);(2);(3);(4).3510233-13624-6233-初步应用巩固知识练习2计算:80205-+;(1)1240568+.--()();(3)189827+-();(2)11323100084832-+.-(4).一定要细心!化简要彻底!细心的同学正确率很高,个别学生今后可要细心呀!本题去括号时要注意符号!{要把小数化成分数再化简!综合应用深化提高练习3化简:.23549+++xxxx223=+++xxxxxx解:原式2223=++xxxx().被开方数由数字换成字母,你是否会算,要注意换元思想的应用。老师:同学们做的挺好的,有个别的同学化简不够熟练,希望今后要多锤炼呀!课堂小结及作业(1)二次根式的加减运算分哪几步进行?每一个步骤的依据是什么?(2)在二次根式的加减中,主要的想法是怎样的?(3)在二次根式加减中,有哪些地方容易出现错误?1、请同学们总结一下本节课所学的知识2、作业:教科书第13页练习2,3;习题16.3第1,2,3题.课题:16.3二次根式的加减(1)一复习旧知例1计算例2计算二、归纳总结:三、应用新知练习1练习2四、巩固新知识五、课堂小结1、2、3、六、作业设置