垂直于弦的直径学案VIP免费

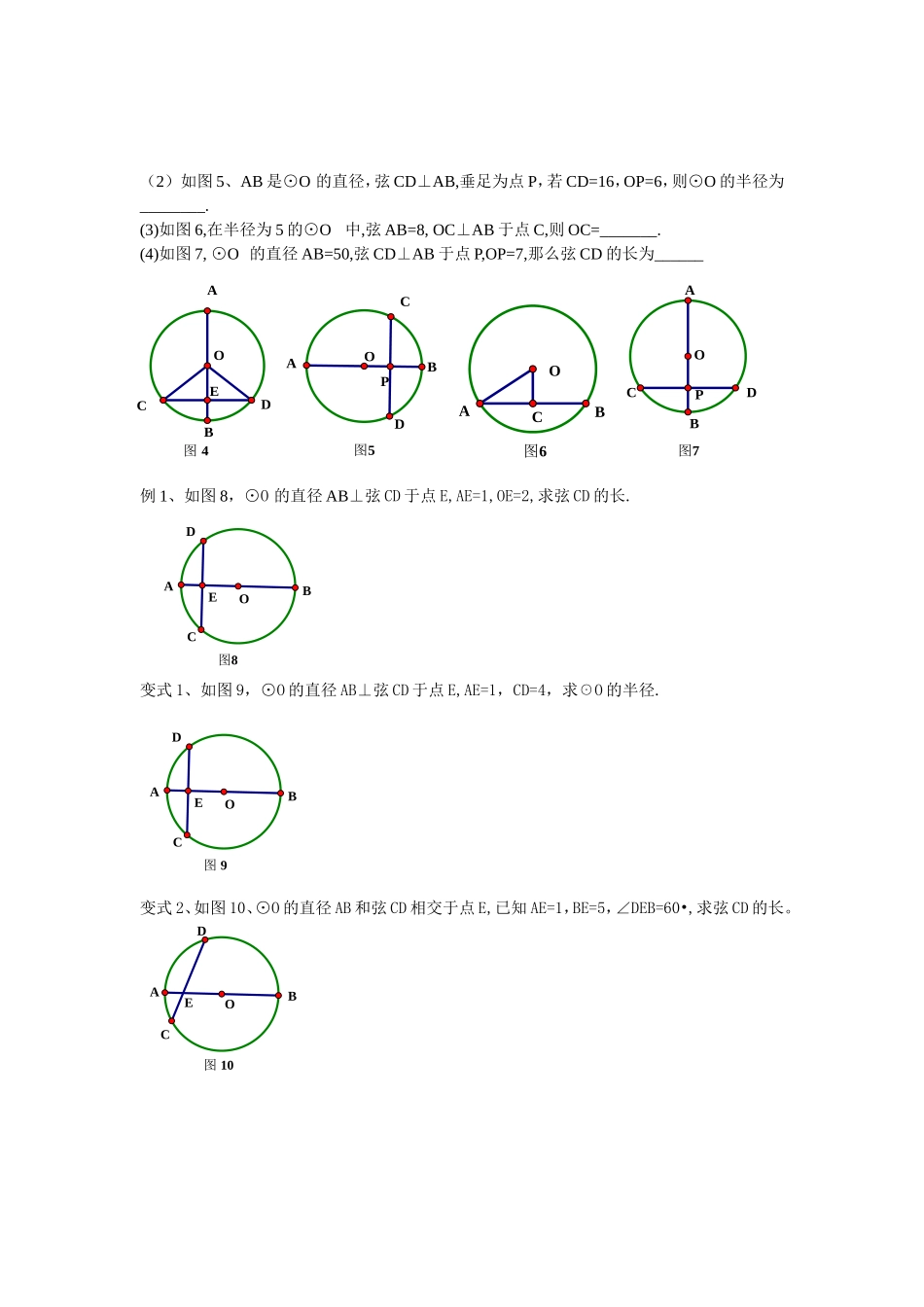
《垂直于弦的直径》学案学习目标：（1）通过观察折纸图片，使学生理解圆的轴对称性。（2）掌握垂直于弦的直径定理，理解其证明过程，学会利用垂直于弦的直径定理解决有关的证明与计算。（3）掌握添辅助线的方法，可以是连半径，或过圆心作一条与弦垂直的线段，目的是找出“半径、半弦、弦心距”组成的直角三角形，进而用勾股定理解题。教学重点：垂直于弦的直径定理及其应用教学难点：垂直于弦的直径定理的证明及其应用学习过程：1、引入新知问1、什么叫轴对称图形？把一个图形沿着某一条直线折叠后，直线两旁的部分能够_________，那么这个图形叫做____________，这条直线叫做________________.2、创设情境问2、圆是轴对称图形吗？如果是，它的对称轴是什么？有多少条？在圆形纸片上用什么方法可以获得对称轴？3、探索新知请同学们在准备好的圆形纸片上画出任意一条直径AB，再画一条弦CD，使得整个图形仍是轴对称图形。请动手折一折。证明:垂直于弦的直径:符号语言:4、运用新知（1）如图4、AB是⊙O的直径，CD为弦，CD⊥AB于点E，则下列结论中不一定成立的是（）CDAB于点PCDABPDCOBADCBOAOBAPDCOBAA、COE=DOEB、CE=DEC、OE=BED、BC=BD（2）如图5、AB是⊙O的直径，弦CD⊥AB,垂足为点P，若CD=16，OP=6，则⊙O的半径为________.(3)如图6,在半径为5的⊙O中,弦AB=8,OC⊥AB于点C,则OC=_______.(4)如图7,⊙O的直径AB=50,弦CD⊥AB于点P,OP=7,那么弦CD的长为______例1、如图8，⊙O的直径AB⊥弦CD于点E,AE=1,OE=2,求弦CD的长.变式1、如图9，⊙O的直径AB⊥弦CD于点E,AE=1，CD=4，求☉O的半径.变式2、如图10、⊙O的直径AB和弦CD相交于点E,已知AE=1，BE=5，∠DEB=60•,求弦CD的长。图8OEDCBA图9OEDCBA图10OEDCBA图4OEDCBA图5PODCBA图7PODCBA图6CBAO