江苏南化一中高三数学一轮教案：三角函数的值域与最值VIP免费

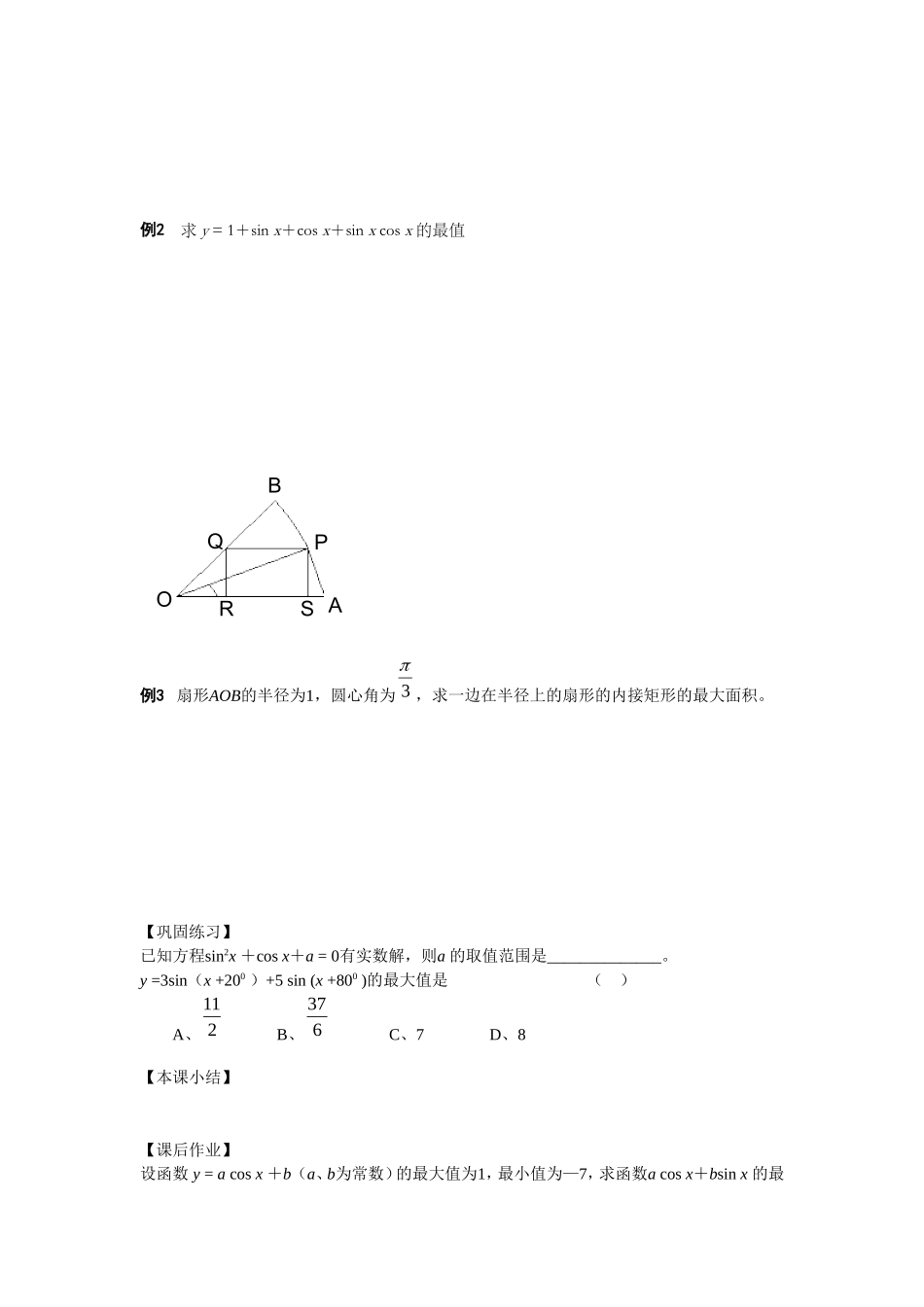
§4.6三角函数的值域与最值【复习目标】根据正、余弦函数的有界性求简单三角函数的最值和值域；运用转化思想，通过变形、换元等方法转化为代数函数求其给定区间内的值域和最值。【重点难点】化归思想及其运用途径【课前预习】函数y=32sinxcosx的最大值是_____，最小值是_____；函数y=24(cos)5x＋1615的最大值是_____，最小值是_____；函数1sin4yx的最大值是，最小值是。若||4x，2()cossinfxxx的最小值是（）A．212B．212C．－1D．122函数y=xsin—2sinx值域是（）A．[—3，—1]B．[—1，3]C．[0，3]D．[—3，0]函数y=log2(1＋sinx)＋log2(1—sinx)，当x[—6，4]时的值域为（）A．[—1，0]B．1,0C．0,1D．[0，1]求下列函数的值域（1）3sin4cosyxx（2）sin3cos()22yxxx【典型例题】例1求下列函数的最值（1）y=21cos2x＋23sinxcosx＋1（xR）；（2）y=2sin1sin3xx例2求y=1＋sinx＋cosx＋sinxcosx的最值SRQPBAO例3扇形AOB的半径为1，圆心角为3，求一边在半径上的扇形的内接矩形的最大面积。【巩固练习】已知方程sin2x＋cosx＋a=0有实数解，则a的取值范围是______________。y=3sin（x+200）+5sin(x+800)的最大值是（）A、211B、637C、7D、8【本课小结】【课后作业】设函数y=acosx＋b（a、b为常数）的最大值为1，最小值为—7，求函数acosx＋bsinx的最大值和最小值。若x(0，)，求函数y=2sin31sin3的最大值。求函数y=(sinx—2)(cosx—2)的最大、最小值。求函数y=2sinxcos（23＋x）＋3cosxsin(＋x)＋sin(2＋x)cosx的周期和值域，并写出使函数y取得最大值的x的集合。已知函数f(x)=2asin2x—23asinxcosx＋a＋b(a0)的定义域为[0，2],值域为[5,1]，求常数a、b的值。设cos2＋3sin2—2sin=0，求y=3sin2＋sin的最大值与最小值．