17.4-一元二次方程根与系数的关系-(第一课时)VIP免费

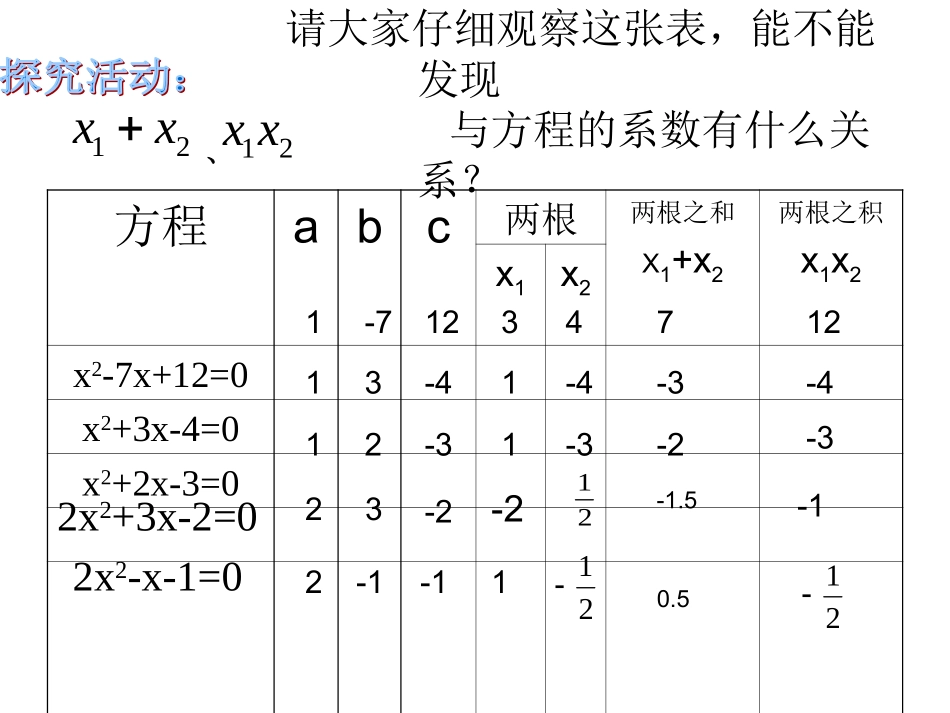
17.4:一元二次方程的根与系数的关系•对课题的思考：•你是如何理解这节课的课题的？（在探讨什么？）•进一步的思考：•探讨一元二次方程的根与系数关系的前提是什么？请大家仔细观察这张表，能不能发现与方程的系数有什么关系？方程abc两根两根之和X1+x2两根之积x1x2x1x2x2-7x+12=0x2+3x-4=0x2+2x-3=011112-43114-4-37-7-212-4-3-3-3322x2+3x-2=02x2-x-1=023-2-2212-1-11212112xx12xx、-1.50.5-1请根据以上的观察发现进一步猜想:方程ax²+bx+c=0(a≠0)的,与系数a,b,c的关系:=―─=─a12xxbc12xxa12xx12xx如果的两个根为、那么：baca12xx12xx此定理是法国数学家韦达首先发现的，也称为韦达定理)0(02acbxax1x2x•对定理的分析：1：利用韦达定理不解方程可直接求出方程二根之和，二根之积的值。而不直接反映方程的二根之差，二根之商与方程的系数之间的关系。2：当b=0时，方程的二根互为相反数，当c=0时，方程必有一根为0.这可以从不同的角度来理解，是相辅相成的。3：利用韦达定理可以求转化为二根之和二根之积的一些常见代数式的值。•使用韦达定理时要注意：1：一元二次方程必须化成一般形式：ax2+bx+c=0(a≠0),以此来确定a.b.c的值。2：注意二根之和为一次项的系数除以二次项的相反数，别忘了前面的负号。3：韦达定理的使用条件是一元二次方程必须要有根，即在△≥0的条件下运用。一：直接说出下列各方程的两根之和与两根之积：1、x2-2x-1=02、2x2-3x+=03、2x2-6x=021x1+x2=2x1x2=-1x1+x2=x1+x2=3x1x2=x1x2=02341二、例题分析：例1：已知关于x方程2x²+kx-4=0的一个根是-4，求它的另一根及k的值242kx解：设方程的另一根是x2，则2442x解方程组，得7212kx例例22方程方程22x2+3x-1=0的两个根记为x1、x2，不解方程，求x12+x22的值4132221xx222121xxxx22222221212121xxxxxxxx21,232121xxxx解：由韦达定理，得∴413212232练习：方程方程x2+3x-1=0的两个根记为x1、x2，不解方程，求的值思考：2111xx020092xx设a,b是方程的两个实数根，则——————的值为baa22小结：1.今天你有什么收获？你还有什么疑问？2.在学习数学的过程中，你学习了哪些数学思想方法？•教学反思：•1：学生在学习根与系数的关系后容易忽视根的判别式的问题，教师应提醒学生注意应用根与系数的关系解题的前提是方程有实数根。•2：学生要对一些常见的代数式能进行熟练变形，进而利用韦达定理求值。