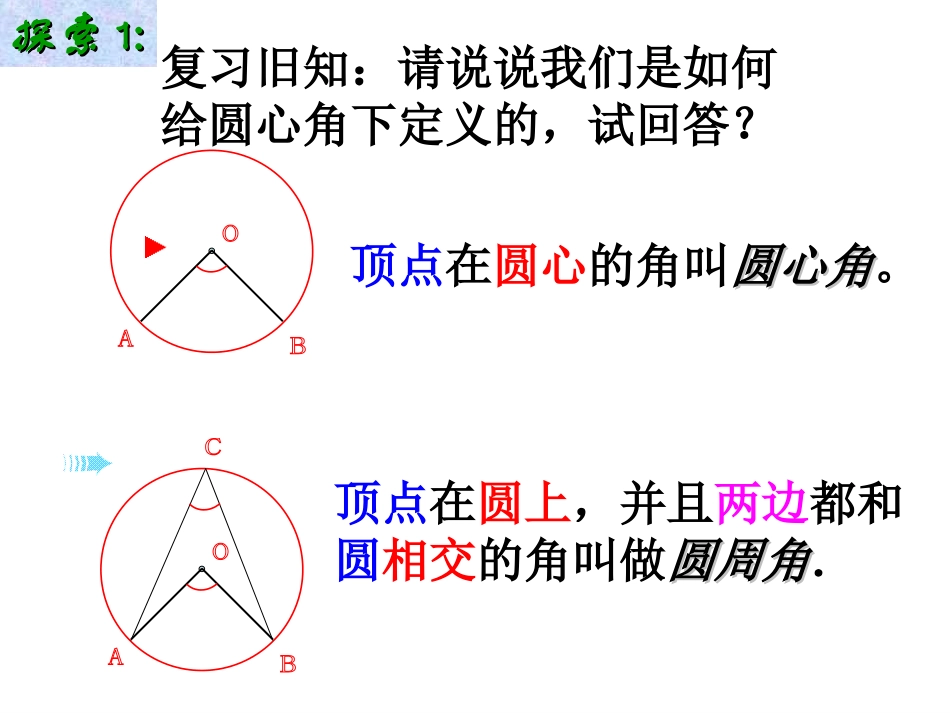
教学目标•1.知道什么是圆周角。•2.理解圆周角定理。•3.会运用圆周角定理进行证明和计算。复习旧知:请说说我们是如何给圆心角下定义的,试回答?顶点在圆心的角叫圆心角圆心角。顶点在圆上,并且两边都和圆相交的角叫做圆周角圆周角.探索探索1:1:探索:判断下列各图中,哪些是圆周角,为什么?画一个圆心角,然后再画同弧所对的圆周角.1.同一条弧你能画多少个圆周角?多少个圆心角?用量角器量一量这些圆周角你有何发现?2.再用量角器量出圆心角的度数,你有何发现呢?发现:一条弧所对的圆周角等于它所对的圆心角的一半.ABO探索探索2:2:发现:在同圆(或等圆)中,同弧或等弧所对的圆周角相等怎样证明同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半?探索探索3:3:分三种情况来证明:(1)圆心在∠BAC的一边上。AOBC∴∠A=C∠证明:∵OA=OC又∵∠BOC=A∠+C∠∴∠BOC=2A∠即∠A=BOC∠21(2)圆心在∠BAC的内部。OABCD1212证明:作直径AD。∵∠BAD=BOD∠∠DAC=DOC∠∴∠BAD+DAC=∠(∠BOD+DO∠C)即:BAC=BOC∠∠1212OABC(3)圆心在∠BAC的外部。D证明:作直径AD。∵∠DAB=DOB∠∠DAC=DOC∠∴∠DAC-DAB=∠(∠DOC-DO∠B)即:BAC=BOC∠∠12121212综上所述,我们可以得到:圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。BOADCE思考:相等的圆周角所对的弧相等吗?在同圆或等圆中,1、求圆中角X的度数BAO.70°xAO.X120°练习练习::2、在⊙O中,∠CBD=30°,BDC=2∠0°,求∠A如图,在⊙O中,AB为直径,CB=CF,弦CGAB⊥,交AB于D,交BF于E求证:BE=EC⌒⌒⌒⌒1.如图,在⊙O中,∠BOC=50°,求∠A的大小。●OBAC解:∠A=∠BOC=25°。21练习练习::2.试找出下图中所有相等的圆周角。ABCD12345678∠2=7∠∠1=4∠∠3=6∠∠5=8∠1.1.圆周角定义:圆周角定义:顶点在圆上顶点在圆上,并且,并且两边都和两边都和圆相交圆相交的角叫圆周角。的角叫圆周角。2.2.在同圆在同圆((或等圆或等圆))中,同弧或等弧所对的中,同弧或等弧所对的圆周角相等圆周角相等,,都等于该弧所对的圆心角的一半;都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等。相等的圆周角所对的弧相等。小结小结::作业作业::习题2.4第2、3两题。