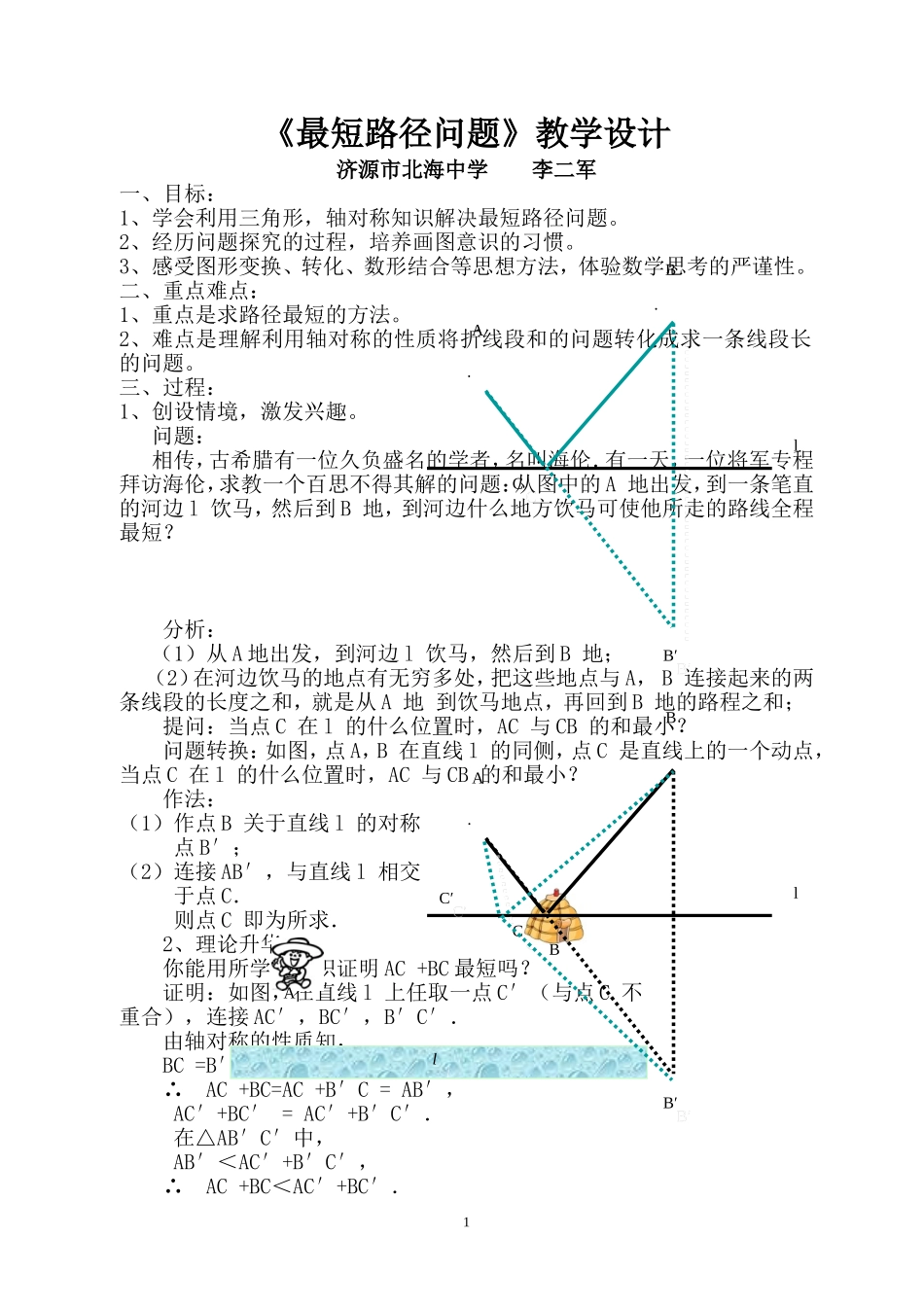
《最短路径问题》教学设计济源市北海中学李二军一、目标:1、学会利用三角形,轴对称知识解决最短路径问题。2、经历问题探究的过程,培养画图意识的习惯。3、感受图形变换、转化、数形结合等思想方法,体验数学思考的严谨性。二、重点难点:1、重点是求路径最短的方法。2、难点是理解利用轴对称的性质将折线段和的问题转化成求一条线段长的问题。三、过程:1、创设情境,激发兴趣。问题:相传,古希腊有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:从图中的A地出发,到一条笔直的河边l饮马,然后到B地,到河边什么地方饮马可使他所走的路线全程最短?分析:(1)从A地出发,到河边l饮马,然后到B地;(2)在河边饮马的地点有无穷多处,把这些地点与A,B连接起来的两条线段的长度之和,就是从A地到饮马地点,再回到B地的路程之和;提问:当点C在l的什么位置时,AC与CB的和最小?问题转换:如图,点A,B在直线l的同侧,点C是直线上的一个动点,当点C在l的什么位置时,AC与CB的和最小?作法:(1)作点B关于直线l的对称点B′;(2)连接AB′,与直线l相交于点C.则点C即为所求.2、理论升华:你能用所学的知识证明AC+BC最短吗?证明:如图,在直线l上任取一点C′(与点C不重合),连接AC′,BC′,B′C′.由轴对称的性质知,BC=B′C,BC′=B′C′.∴AC+BC=AC+B′C=AB′,AC′+BC′=AC′+B′C′.在△AB′C′中,AB′<AC′+B′C′,∴AC+BC<AC′+BC′.1BAllB·lA·B′B′CCB·lA·B′B′CCC′C′﹒﹒A〞AAMNaabb﹒﹒A〞AAMNaabb﹒﹒A〞AAA′A′MNaabbOO﹒﹒A〞AAA′A′MNaabbOOabAB﹒﹒A′B′MNabAB﹒﹒A′B′MN即AC+BC最短.3、拓展延伸1、牧童家在A处。现在牧童要先带马到河(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回家。问:牧童让马在何处饮水?2、有同学提出直接走到O处既能喝水又能吃草,这样的路径最短,你同意吗?请说出理由。3、牧童家在A处。现在牧童要先带马到河(图中用直线a表示)饮水,再到草地(图中用直线b表示)吃草,然后回姥姥家B处。问:牧童让马在何处饮水、吃草?三、课堂小结课堂小结知识方法思想归纳知识方法思想归纳::11、平面图形上不在同一直线上的最短路径问、平面图形上不在同一直线上的最短路径问题,可以通过平移、对称等方法,将其转移到同一直线上来,题,可以通过平移、对称等方法,将其转移到同一直线上来,利用利用两点之间,线段最短以及勾股定理等知识来解决.两点之间,线段最短以及勾股定理等知识来解决.22、以上都体现了转化的数学思想、以上都体现了转化的数学思想四、作业布置四、作业布置11、请你提出一个运用两点之间线段最短、勾股定理知识,运用对称来解、请你提出一个运用两点之间线段最短、勾股定理知识,运用对称来解决的问题,并解答.决的问题,并解答.22、数学书第、数学书第114114页页55、、662