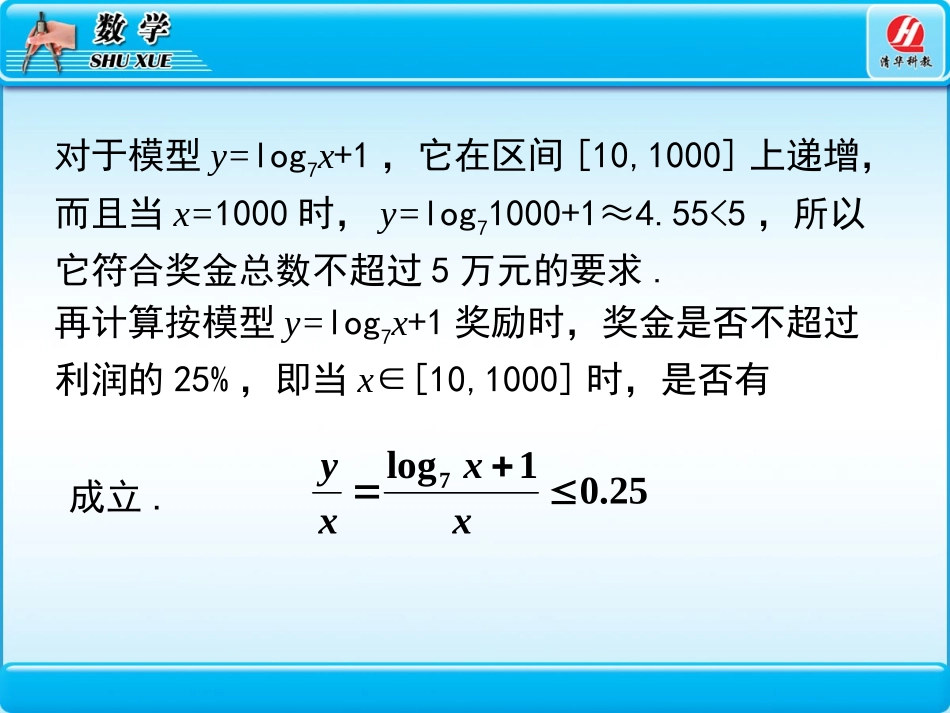
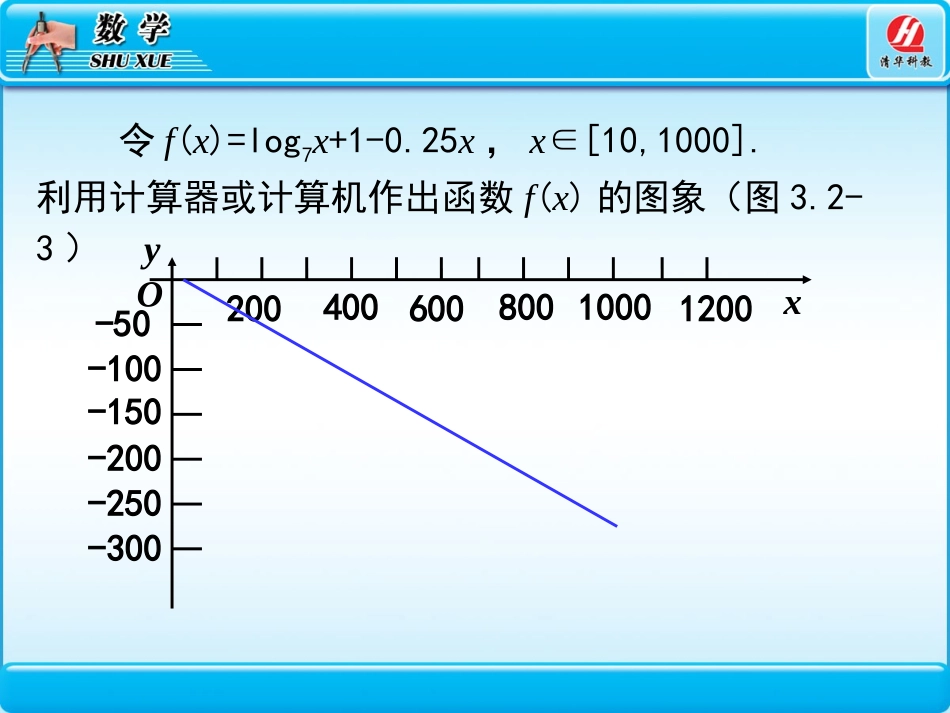
首先计算哪个模型的奖金总数不超过5万.对于模型y=0.25x,它在区间[10,1000]上递增,而且当x=20时,y=5,因此,当x>20时,y>5,所以该模型不符合要求;对于模型y=1.002x,由函数图象,并利用计算器,可知在区间(805,806)内有一个点x0满足,由于它在区间[10,1000]上递增,因此当x>x0时,y>5,所以该模型也不符合要求;5002.10x对于模型y=log7x+1,它在区间[10,1000]上递增,而且当x=1000时,y=log71000+1≈4.55<5,所以它符合奖金总数不超过5万元的要求.再计算按模型y=log7x+1奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有25.01log7xxxy成立.令f(x)=log7x+1-0.25x,x∈[10,1000].利用计算器或计算机作出函数f(x)的图象(图3.2-3)20040060080010001200-250-300-200-150-100-50Oxy由图象可知它是递减的,因此f(x)
x2,有时2xlog2x.3.说说函数y=2x,y=x2,y=log2x的增长差异.在区间(0,+∞)上,总有x2>log2x;当x>4时,总有2x>x2.所以当x>4时,总有2x>x2>log2x.4.一般的,在区间(0,+∞)上,尽管函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个‘档次’上,随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就有logaxx0时,总有xxyx2121log2.),0()10(log),0(),10(上的衰减情况在区间最后探究axynxyaayanx在区间(0,+∞)上,总存在一个x0,当x>x0时,总有xn>ax>logax(n<0,0