相似三角形预备定理VIP免费

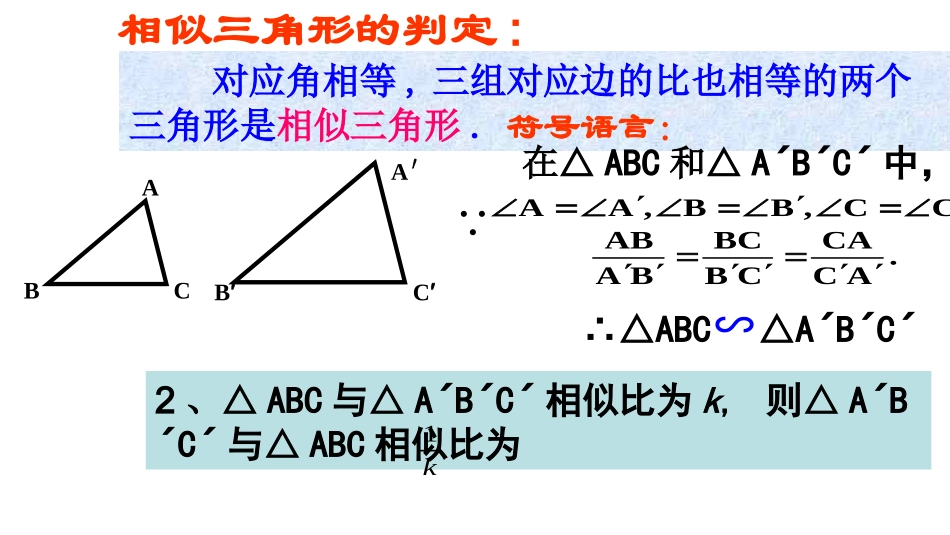
27.2相似三角形的判定1预备定理相似多边形的判定：回顾：对应角相等，对应边的比相等的两个多边形为相似多边形.两个条件要同时具备对应角相等,三组对应边的比也相等的两个三角形是相似三角形.相似三角形的判定:2、△ABC与△ABC´´´相似比为k,则△AB´C´´与△ABC相似比为AC′B′A′CB∴△ABC∽△ABC´´´.ACCACBBCBAABCC,BB,AA 1k符号语言：在△ABC和△ABC´´´中，对应角_______,对应边——————的两个三角形,叫做相似三角形.相等比相等相似三角形的———————,各对应边—。对应角相等比相等∠A=D,B=E,C=F∠∠∠∠∠EFBCDFACDEABA△ABC∽DEF△BCDFE相似比:=kDFACEFBCDEABk1两三角形相似k=1两三角形全等问题二问题二如何不通过测量，运用所学知识，快速将一根绳子如何不通过测量，运用所学知识，快速将一根绳子分成两部分，使这两部分之比是分成两部分，使这两部分之比是2:3?2:3?AABBCCEEDDFFBBIDDICCIEEIFFI32CCIFFI则ACACIEFDEBCAB与如图，任意画两条直线l1、l2,再画三条与l1、l2相交的平行线l3、l4、l5.分别度量l3、l4、l5在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度.相等吗？ABCDEFl1l2l3l4l5任意平移l5，再度量AB,BC，DE,EF的长度.相等吗？EFDEBCAB与探究：定理的符号语言定理的符号语言L3//L4//L5==ABDEBCEF(平行线分线段成比例定理)三条平行线截两条直线,所得的对应线段的比相等.DEFABCL3L4L5L1L2AABBCCDDEEFFll11ll33ll22下上下上全下全下右左右左................形象记忆形象记忆求：BC.4.EF2,DE3,，AB//l//l已知：如图，l321AABBCCDDEEFFll11ll33ll223?42[[例例一一]][[例例一一]]（平行线分线段成比例定理）6BC42BC3即EFDEBCAB//l//ll解：321AABBCCDDEEFFll11ll33ll22.nmmDFDE求证：.nmBCAB，//l//l已知：如图，l321[[例例二二]][[例例二二]]注意观察：注意观察：此图与前面图形有何不同？此图与前面图形有何不同？AABBCCDDEEFF（平行线分线段成比例定理）.nmmDFDE.mnmDEDF即，mmnDEDEEFmnDEEFnmEFDEBCAB,//l//ll321：证明AABBCCDDEEFFAABBCCDDEEFFAABBCCDDEEFFAABBCCDDEEFFAABBCCDDEEFFABCDEl1l2l3l4l5ABCDEl1l2l3l4l5如图，l3l∥4l∥5,请指出成比例的线段.练习：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段的比相等.ABCDEl1l2l3l4l5ABCDEl1l2l3l4l5L1L2L3L4L5L1L2L3L4L5ABCEDABCDE DEBC∥ADADAEAEACACABAB= DEBC∥ADADAEAEACACABAB= 数学符号语言数学符号语言平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段的比相等三角形的中位线截得的三角形与原三角形是否相似？相似比是多少？ABCDE提出问题：如图，在∆ABC中，点D是边AB的中点，DEBC∥，DE交AC于点E，∆ADE与∆ABC有什么关系？BCADE思考:改变点D在AB上的位置，请猜想∆ADE与∆ABC是否相似?说明理由.如图,在△ABC中,DE//BC,DE分别交AB,AC于点D,E,△ADE与△ABC有什么关系?思考？直觉告诉我们,△ADE与△ABC相似,我们通过相似的定义证明这个结论.先证明两个三角形的对应角相等.在△ADE与△ABC中,∠A=∠A, DE//BC,∴∠ADE=∠B,∠AED=∠C.再证明两个三角形的对应边的比相等.过E作EF//AB,EF交BC于F点.在平行四边形BFED中,DE=BF,DB=EF.//,//,,DEBCEFABADAEBFAEABACBCACDEFBDEAEBCACADAEDEABACBC四边形是平行四边形，DE=BF即:△ADE与△ABC中,∠A=A,ADE=B,AED=C.∠∠∠∠∠∴△ADE∽△ABCADAEDEABACBC相似三角形的预备定理：平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似。△ADEABC∽△DE//BCEDCBAEDCBAEDCBA平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。判定三角形相似的预备定理：（简称：平行线）在△ABC中， DEBC∥∴△ADE∽△ABC符号语言：ABCDE（图1）（图2）DEOBC“A”型“X”型1、如图,已知EF∥CD∥AB，请尽可能多地找出图中的相似三角形，并说明理由。练习：三角形相似具有三角形相似具有传递性传递性!!1.EF∥A...