反比例函数的图像与性质VIP免费

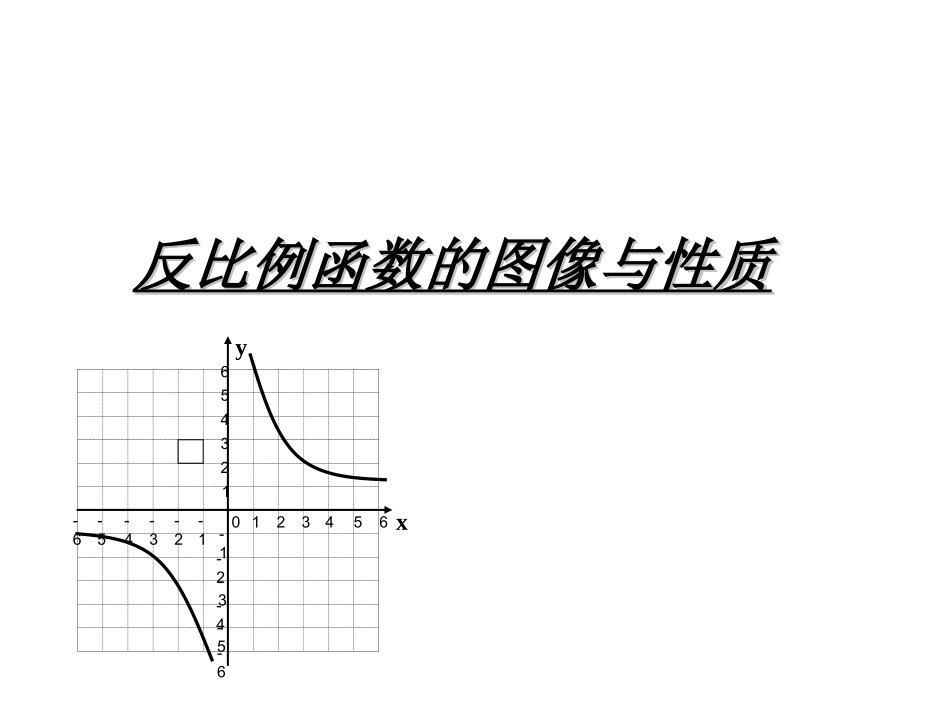
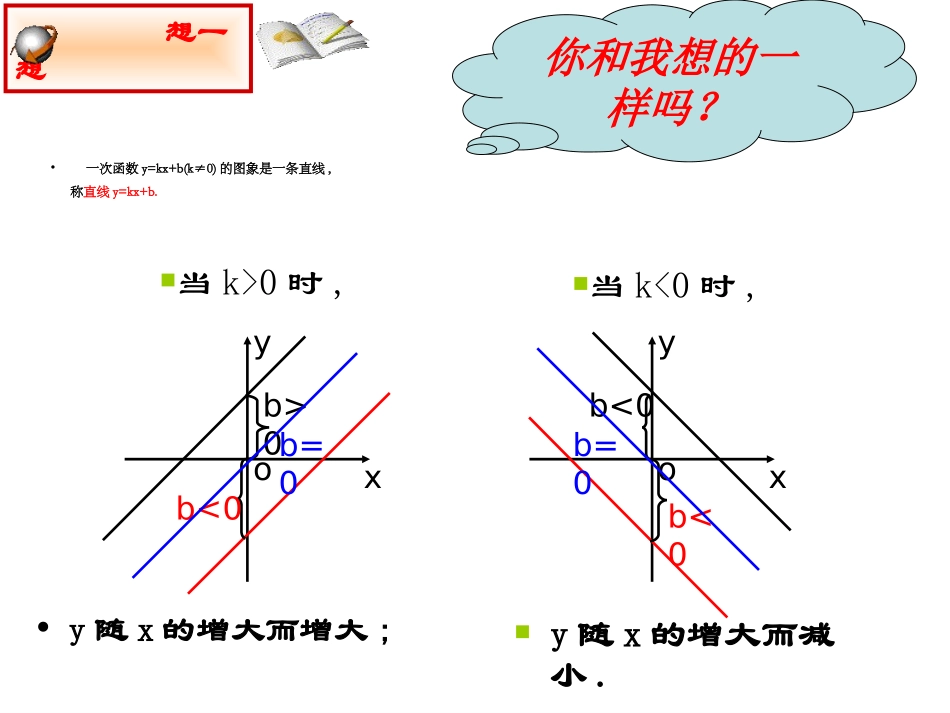
123456-1-3-2-4-5-61234-1-2-3-40-6-556xy反比例函数的图像与性质反比例函数的图像与性质想一想你还记得一次函数y=kx+b(k≠0)的图象与性质吗?你还记得作函数图象的一般步骤吗？反比例函数的图像又是什么样子呢？有何性质？想一想•一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.•y随x的增大而增大;xyoxyoy随x的增大而减小.b<0b>0b=0b<0b<0b=0当k>0时,当k<0时,你和我想的一样吗？用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).活动一：自己动手做P147，向同学们展示自己的收获。画出反比例函数和的函数图象。y=x6y=x6心动不如行动123456-1-3-2-4-5-61234-1-2-3-40-6-556yxxy=x6y=x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……y=x6y=-x6•列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;•列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;•连线时一定要养成按自变量从小到大的顺序，依次用平滑的曲线连接,从中体会函数的增减性；•……议一议你认为作反比例函数图象时应注意哪些问题？K>0K<0当k＞0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小.当k＜0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大.2.图象性质见下表：图象性质y=xk反比例函数的图象和性质：基础训练1、请指出下面的图像中那一个是反比例函数的图像（C）思考与练习思考与练习A：xyoB：xyoD：xyoC：xyo2、反比例函数y=-的图象大致是:x5(c)3、（1）已知反比例函数若函数的图象位于第一三象限，则k______;4kyx<4（2）函数y=kx-k与在同一条直角坐标系中的图象可能是:0kykxxyoxyoxyoxyo(A)(B)(C)(D)思考与练习(D)结束寄语•函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.•函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.下课了!作业：课本150页习题5.2必做题第1、2题随堂练习149页独立作业驶向胜利的彼岸