二次函数的图像和最值VIP免费

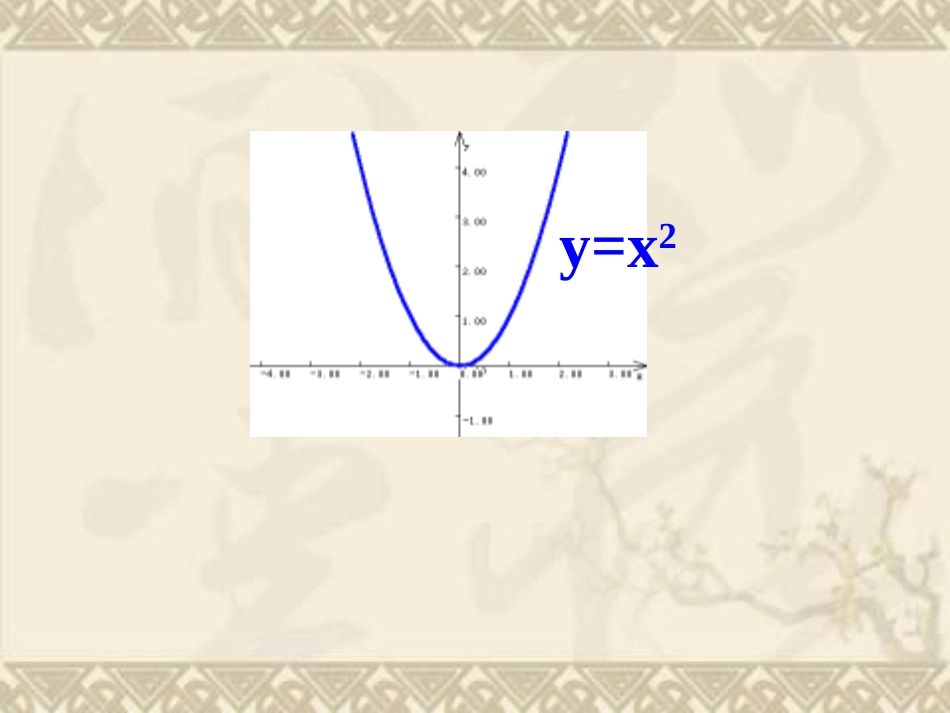
二次函数的图像和最值画出下列函数的图象,并(1)y=x2(2)y=x2+1(3)y=x2－1说明它们的关系:基础练习y=x21作函数的图象的常用方法描点作图法;变换作图法.y=x2y=x2+1y=x2y=x2+1y=x2－1函数y=f(x)+k与函数y=f(x)图象间的关系:当k＞0时,把函数y=f(x)的图象向上平移k个单位即得函数y=f(x)+k的图象.(k＜0)(向下)(－k)简称:上+下－画出下列函数的图象,并说明它们的关系:(1)y=x2(2)y=(x+2)2(3)y=(x－2)2基础练习y=x2y=x2y=(x+2)2y=x2y=(x+2)2y=(x－2)2函数y=f(x+m)与函数y=f(x)图象间的关系:当m＞0时,把函数y=f(x)的图象向左平移m个单位即得函数y=f(x+m)的图象.(m＜0)(向右)(－m)简称:左+右－画出函数y=(x+3)2－2的图象.课堂练习y=x2y=x2y=(x+3)2y=x2y=(x+3)2y=(x+3)2－2画出下列函数的图象,并基础练习说明它们的关系:(1)y=3x+4(2)y=－3x+4y=3x+4y=3x+4y=－3x+4函数y=f(－x)与函数y=f(x)图象间的关系:函数y=f(－x)的图象与函数y=f(x)的图象关于y轴对称.画出下列函数的图象,并基础练习说明它们的关系:(1)y=x2－x(2)y=2xxy=x2－xy=x2－x(x≤0或x≥1)y=2xx函数y=与函数y=f(x)图象间的关系:()fx保留函数y=f(x)在x轴的上方的图象,把它在x轴的下方的图象沿x轴翻折,即得到y=的图象.()fx变换作图法平移变换对称变换画出下列函数的图象:(1)y=x2+2+1(2)y=x22xx2二次函数在闭区间上的最值问题求给定区间x∈[m，n]的二次函数y=f(x)=ax2+bx+c（a≠0）最值步骤（1）配方。（2）画图象。（3）根据图象确定函数最值。（看所给区间内的最高点和最低点）练习：已知函数f(x)=x2–2x–3（1）若x∈[–2，0]，求函数f(x)的最值；（2）若x∈[2，4]，求函数f(x)的最值；（3）若x∈[]，求函数f(x)的最值；25,2123,21（4）若x∈[]，求函数f(x)的最值；练习：已知函数f(x)=x2–2x–3.（1）若x[∈–2，0],求函数f(x)的最值；解：画出函数在定义域内的图像如图对称轴为直线x=1由图知，y=f(x)在[–2，0]上为减函数故x=-2时有最大值f(-2)=5x=0时有最小值f(0)=-3642240-2x=1∙∙例1、已知函数f(x)=x2–2x–3.（1）若x[∈–2，0]，求函数f(x)的最值；（2）若x[∈2，4]，求函数f(x)的最值；解：画出函数在定义域内的图像如图对称轴为直线x=1由图知，y=f(x)在[2，4]上为增函数故x=4时有最大值f(4)=5x=2时有最小值f(2)=-3642245x=142∙∙例1、已知函数f(x)=x2–2x–3.（1）若x∈[–2，0]，求函数f(x)的最值；（2）若x∈[2，4]，求函数f(x)的最值；（3）若x∈[],求函数f(x)的最值；25,21解：画出函数在定义域内的图像如图对称轴为直线x=1,由图知，x=时有最大值x=1时有最小值f(1)=-45253()124f4224x=15212∙∙例1、已知函数f(x)=x2–2x–3（1）若x∈[–2，0]，求函数f(x)的最值；（2）若x∈[2，4]，求函数f(x)的最值；（3）若x∈[]，求函数f(x)的最值；25,2123,21（4）若x∈[]，求函数f(x)的最值；解：画出函数在定义域内的图像如图对称轴为直线x=1,由图知，x=时有最大值x=1时有最小值f(1)=-41213()124f4224x=132-12∙∙例1、已知函数f(x)=x2–2x–325,2123,21（4）x∈[]（1）x∈[–2，0]（2）x∈[2，4]（3）x∈[]642240-2x=1∙∙642245x=142∙∙4224x=15212∙∙4224x=132-12∙∙思考：通过以上几题，你发现二次函数在区间[m，n]上的最值通常在哪里取到？总结：求二次函数f(x)=ax2+bx+c在[m，n]上上的最值或值域的一般方法是：（2）当x0∈[m，n]时，f(m)、f(n)、f(x0）中的较大者是最大值,较小者是最小值；（1）检查x0=是否属于[m，n]；ab2（3）当x0[m，n]时，f(m)、f(n)中的较大者是最大值，较小者是最小值.例2：若x∈，求函数y=x2+ax+3的最小值：11xxO1xy-1例2：若x∈，求函数y=x2+ax+3的最小值：11xx-11Oxy例2：若x∈，求函数y=x2+ax+3的最小值：11xx-11Oxy例2：若x∈，求函数y=x2+ax+3的最小值：11xxOxy1-1⑴当即a≥2时12ay的最小值为f(-1)=4-a解：例3：若x∈，求函数y=x2+ax+3的最小值：11xxOxy1-1(2)当即-2≤a<2时2ay的最小值为f()=432a121a例2：若x∈，求函数y=x2+ax+3的最小值：11xxOxy1-1(3)当即a<-2时12ay...