实数与二次根式VIP免费

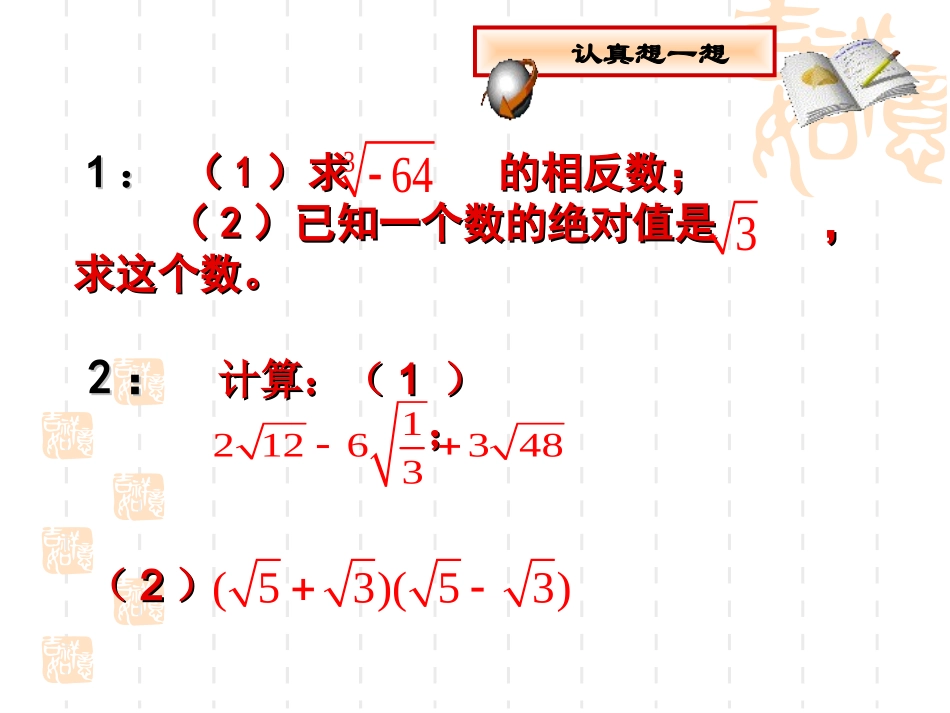
中考总复习中考总复习实数与二次根式实数与二次根式郧县南化中学刘正成郧县南化中学刘正成【内容指要】【内容指要】11．了解平方根、算术平方根、立方根的概．了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根、立方根．念，会用根号表示数的平方根、立方根．22．会用平方运算求某些非负数的平方根，．会用平方运算求某些非负数的平方根，会用立方运算求某些数的立方根，会用计算会用立方运算求某些数的立方根，会用计算器求平方根和立方根．器求平方根和立方根．33．了解二次根式的概念及其加、减、乘、．了解二次根式的概念及其加、减、乘、除运算法则，会用它们进行有关实数的简单除运算法则，会用它们进行有关实数的简单四则运算（分母有理化）．四则运算（分母有理化）．共同记一记11：：（（11）求的相反数；）求的相反数；（（22）已知一个数的绝对值是，）已知一个数的绝对值是，求这个数。求这个数。22：：计算：（计算：（11））；；（（22））认真想一想3643121263483(53)(53)二次根式的概念二次根式的概念形如形如（（aa00））的式子的式子叫做二次根式叫做二次根式a１．二次根式的定义：１．二次根式的定义：２．二次根式的识别：２．二次根式的识别：（１）．被开方数（１）．被开方数（２）．根指数是２（２）．根指数是２0a例例11．下列各式中那些是二次根式？那些不是？．下列各式中那些是二次根式？那些不是？为什么？为什么？153a100x3522ab21a144221aa⑧⑧⑦⑦⑥⑥⑤⑤④④①①②②③③例2.x为何值时，下列各式在实数范围内有意义。32)1(xx31)2(2)5()3(x1)4(2x123)5(xx12)6(0)6(5)7(xx变式练习：2、已知求算术平方根。977xxy2)64(xy1、能使二次根式有意义的实数x的值有（）A、0个B、1个C、2个D、无数个2)2(xB3、已知x、y是实数，且求3x+4y的值。214422xxxy二次根式性质及运算律1)20aaa2)2||aa00aaaa乘除)0b,0a(baba)0b,0a(baab（一）二次根式的性质（二）二次根式的运算二次根式的性质aa2).(1)0(aaaa2.2)0(a)0(a例：计算2)32)(1(2)621)(2(2)32)(3(2)3)(4(x变式应用1、式子成立的条件是（）1)1(2aa1.aA1.aB1.aC1.aDD2、已知三角形的三边长分别是a、b、c，且，那么等于（）A、2a-bB、2c-bC、b-2aD、b-2Cca2)(bcaacD例、把下列各式写成平方差的形式，再（在实数范围内）分解因式；54)1(2x9)2(4a103)3(2a96)4(24aa例5、已知互为相反数，求a、b的值。86baba与例7、化简22)2()4(xx例例66、已知＋、已知＋|2|2xx－－33yy－－18|18|＝＝00，求，求xx－－66yy的立方根．的立方根．211xy二次根的乘除)0,0(babaab1、积的算术平方根的性质2、二次根式的乘法法则)0,0(baabba例1、化简8116)1(2000)2(例2、计算721)1(15253)2()521(154)3(xyx11010)4(变式应用1、成立的条件是。44162xxx4x3、商的算术平方根的性质4、二次根式的除法法则)0,0(bababa)0,0(bababa例3、计算4540)1(245653)2(nmnm5、最简二次根式的两个条件：（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式；化简二次根式的方法:：（1）如果被开方数是整数或整式时，先因数分解或因式分解,然后利用积的算术平方根的性质,将式子化简。（2）如果被开方数是分数或分式时,先利用商的算术平方根的性质,将其变为二次根式相除的形式,然后利用分母有理化,将式子化简。例4、判断下列各式中哪些是最简二次根式，哪些不是？为什么？ba23)1(ab5.1)2(22)3(yxba)4(练习：把下列二次根化为最简二次根式。12)1(48)2(125)3(800)4(23)5(81)6(533)7(4.0)8(243)9(121)10(523)11(二次根式的加减1、同类二次根式几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根就叫做同类二次根式。2、二次根式的加减（1）先化简，（2）再合并。例1、计算32411821182)1(4832714122)2(ababaabba222)3(二次根式的...