椭圆及其标准方程PPTVIP免费

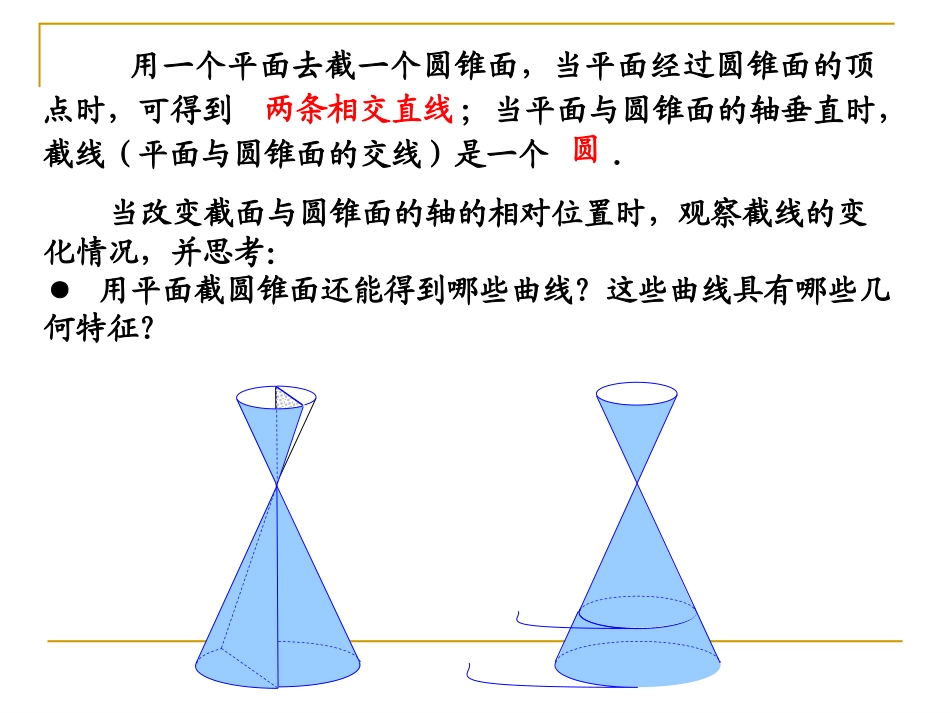
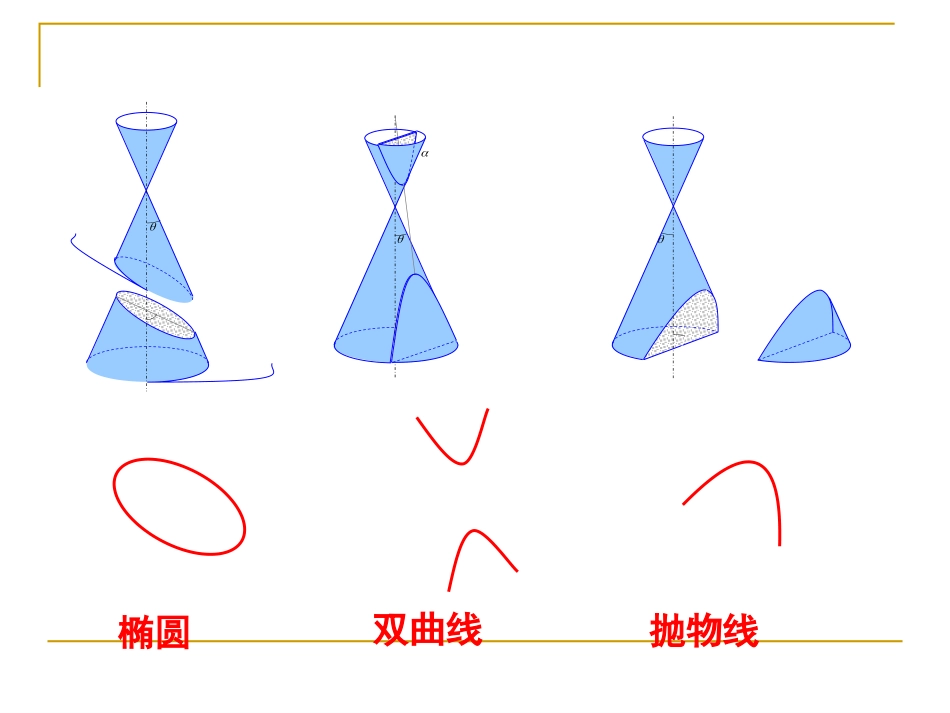
第二章圆锥曲线与方程第二章圆锥曲线与方程§2.1.1§2.1.1椭圆及其标准方程椭圆及其标准方程第二章圆锥曲线与方程第二章圆锥曲线与方程§2.1.1§2.1.1椭圆及其标准方程椭圆及其标准方程用一个平面去截一个圆锥面，当平面经过圆锥面的顶点时，可得到；当平面与圆锥面的轴垂直时，截线（平面与圆锥面的交线）是一个．当改变截面与圆锥面的轴的相对位置时，观察截线的变化情况，并思考：●用平面截圆锥面还能得到哪些曲线？这些曲线具有哪些几何特征？两条相交直线圆椭圆双曲线抛物线一、引入结论：平面内到两定点F1，F2的距离之和等于常数的点的轨迹为椭圆。常数必须大于两定点的距离1、椭圆的定义：平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的动点M的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距|F1F2|=2c。1F2FM几点说明：1、椭圆定义式：|MF1|+|MF2|=2a>|F1F2|=2c.则M点的轨迹是椭圆.2、若|MF1|+|MF2|=2a=|F1F2|=2c，则M点的轨迹是线段F1F2.3、若|MF1|+|MF2|=2a<|F1F2|=2c，则M点的轨迹不存在.二、讲授新课应用举例例1.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解(1)因|MF1|+|MF2|=6>|F1F2|=4，故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4，故点M的轨迹不是椭圆(是线段F1F2)。(3)因|MF1|+|MF2|=3<|F1F2|=4，故点M的轨迹不成图形。OxyF1F2M如图所示：F1、F2为两定点，且|F1F2|=2c，求平面内到两定点F1、F2距离之和为定值2a（2a>2c)的动点M的轨迹方程。解：以F1F2所在直线为X轴，线段F1F2的垂直平分线为Y轴，建立平面直角坐标系，则焦点F1、F2的坐标分别为(-c,0)、(c,0)。(-c,0)(c,0)(x,y)设M（x,y)为所求轨迹上的任意一点，则:|MF1|+|MF2|=2a且2a>2caycxycx2)()(:2222即2、椭圆标准方程及其推导2、椭圆标准方程及其推导求曲线轨迹方程的步骤：1、建系2、设标3、列式4、化简5、检验（可省略不写）OXYF1F2M(-c,0)(c,0)(x,y)两边平方得：a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即：(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c，即a>c，所以a2-c2>0，令a2-c2=b2，其中b>0，代入上式可得：12222byax2222)(2)(ycxaycx所以2222222)()(44)(:ycxycxaaycx两边平方得222)(:ycxacxa即b2x2+a2y2=a2b2两边同时除以a2b2得：(a>b>0)这个方程叫做椭圆的标准方程，它所表示的椭圆的焦点在x轴上。acbOXYF1F2M(-c,0)(c,0)OXYF1F2M(0,-c)(0,c))0(12222babyax)0(12222babxay椭圆的标准方程的几点说明：（1）椭圆标准方程的形式：左边是两个分式的平方和，右边是1（2）椭圆的标准方程中三个参数a、b、c满足a2=b2+c2。（3）椭圆的标准方程中：x2与y2的分母哪一个大，则焦点在哪一条轴上，大分母为a2，小分母为b2.椭圆的标准方程2222+=1>>0xyabab2222+=1>>0xyabba分母哪个大，焦点就在哪个轴上12-,0,0，FcFc120,-0,，FcFc标准方程相同点焦点位置的判断不同点图形焦点坐标定义a、b、c的关系a2-c2=b23、椭圆的标准方程小结|MF1|+|MF2|=2a(2a>2c>0)12yoFFMxyxoF2F1M例2.已知椭圆的两个焦点坐标分别为（-2，0），53（2，0）并且经过点（，-），求它的标准方程.22例3、椭圆的两个焦点的坐标分别是（－4，0），（4，0），椭圆上一点P到两焦点距离之和等于10，求椭圆的标准方程。例4、动点P到两定点F1(-4,0)，F2(4,0)的距离之和为8，则动点P的轨迹为（）A.椭圆B.线段F1F2C.直线F1F2D.不能确定B例例55、椭圆上一点、椭圆上一点PP到一个焦点的距离等于到一个焦点的距离等于33，则，则它到另一个焦点的距离是（）它到另一个焦点的距离是（）A.5B.7C.8D.2A.5B.7C.8D.22212516xyB例6、动点P到两定点F1(-4,0)，F2(4,0)的距离和是7，则动点P的轨迹为（）A.椭圆B.线段F1F2C.直线F1F2D.无轨迹D例2.已知椭圆的两个焦点坐标分别是(-2,0),(2,0),并且经过点,求它的标准方程.)23,25(解法一:因为椭圆的焦点在x轴上,所以...