柱体锥体台体球体体积VIP免费

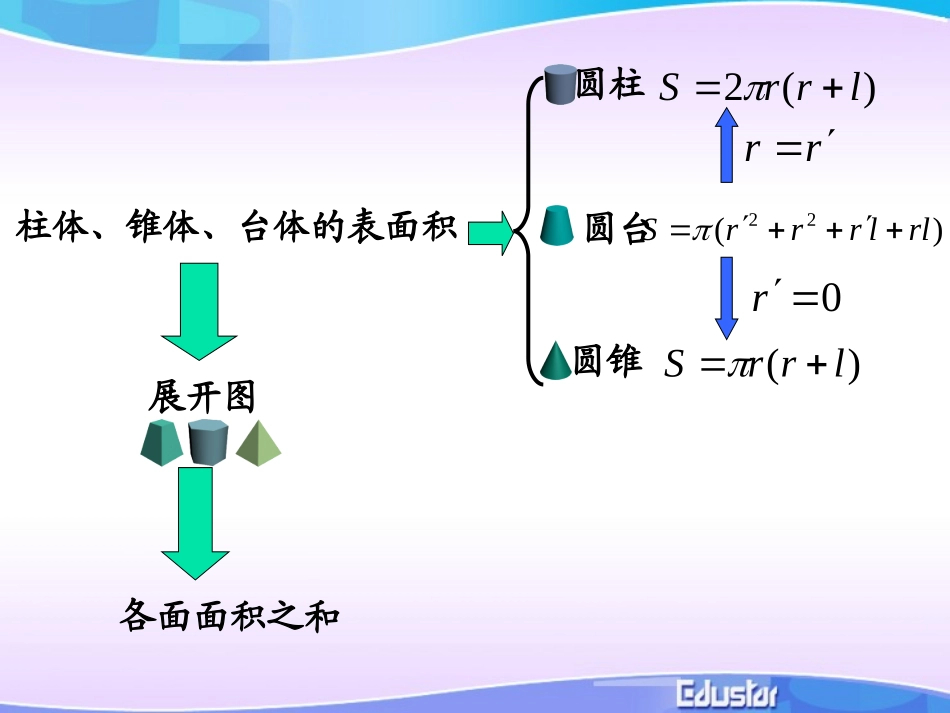
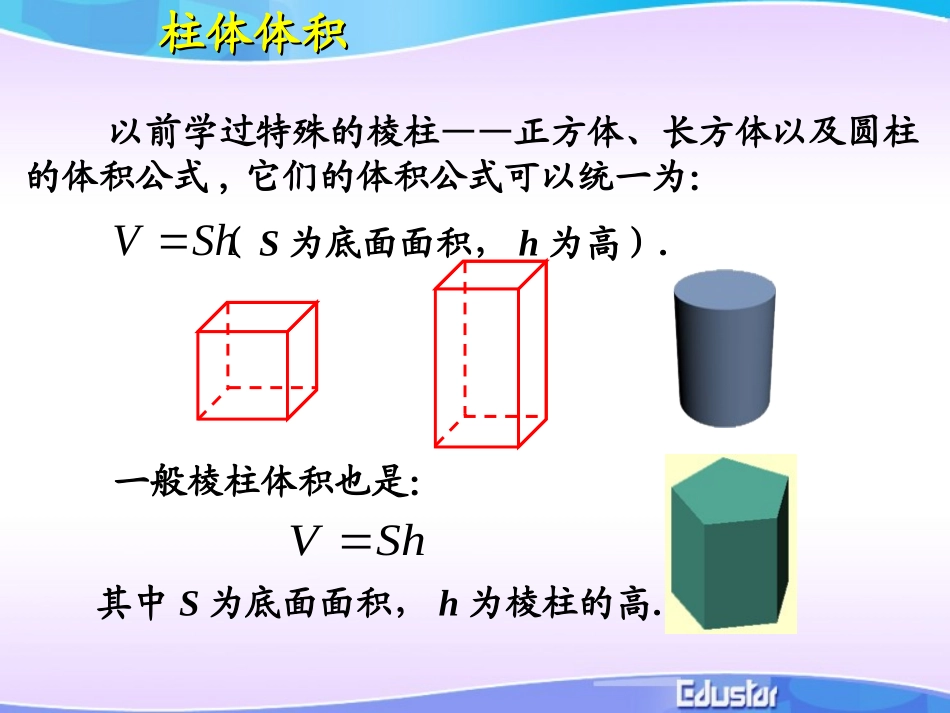
1.3.11.3.1柱体、锥体、台体，球体的体积柱体、锥体、台体，球体的体积柱体、锥体、台体的表面积各面面积之和rr0r展开图)(22rllrrrS圆台圆柱)(2lrrS)(lrrS圆锥以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为：ShV（S为底面面积，h为高）．柱体体积柱体体积一般棱柱体积也是：ShV其中S为底面面积，h为棱柱的高．圆锥的体积公式：ShV31（其中S为底面面积，h为高）圆锥体积等于同底等高的圆柱的体积的．31圆锥体积圆锥体积探究棱锥与同底等高的棱柱体积之间的关系．棱锥体积棱锥体积三棱锥与同底等高的三棱柱的关系ShV31（其中S为底面面积，h为高）由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱锥与圆锥的体积公式类似，都是等于底面面积乘高的．31经过探究得知，棱锥也是同底等高的棱柱体积的．即棱锥的体积：31锥体体积锥体体积台体体积台体体积由于圆台(棱台)是由圆锥(棱锥)截成的，因此可以利用两个锥体的体积差．得到圆台(棱台)的体积公式(过程略)．根据台体的特征，如何求台体的体积？ABABCDCDPSShDCBAPABCDPVVVhSSSS)(31棱台（圆台）的体积公式hSSSSV)(31其中，分别为上、下底面面积，h为圆台（棱台）的高．SS台体体积台体体积柱体、锥体、台体的体积公式之间有什么关系？hSSSSV)(31S为底面面积，h为柱体高ShV0SS分别为上、下底面面积，h为台体高ShV31SSS为底面面积，h为锥体高台体体积台体体积上底扩大上底缩小例3有一堆规格相同的铁制（铁的密度是）六角螺帽共重5.8kg，已知底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（取3.14）？3/8.7cmg解：六角螺帽的体积是六棱柱的体积与圆柱体积之差，即:10)210(14.3106124322V)(29563mm)(956.23cm所以螺帽的个数为252)956.28.7(10008.5（个）答：这堆螺帽大约有252个．典型例题典型例题怎样求球的体积?怎样求球的体积?h实验：排液法测小球的体积h实验：排液法测小球的体积h实验：排液法测小球的体积h实验：排液法测小球的体积h实验：排液法测小球的体积h实验：排液法测小球的体积h实验：排液法测小球的体积hH小球的体积小球的体积等于等于它排开液体的它排开液体的体积体积实验：排液法测小球的体积曹冲称象学习球的知识要注意和圆的有关指示结合起来．所以我们先来回忆圆面积计算公式的导出方法．我们把一个半径为R的圆分成若干等分，然后如上图重新拼接起来，把一个圆近似的看成是边长分别是.的矩形和RR.2R于那么圆的面积就近似等回顾圆面积公式的推导当所分份数不断增加时，精确程度就越来越高；当份数无穷大时，就得到了圆的面积公式．法导出球的体积公式下面我们就运用上述方分割求近似和化为准确和割圆术,21RRr,)(222nRRr已知球的半径为R,用R表示球的体积.,)2(223nRRrAOB2C2球的体积AOOR)1(inR半径：“”层小圆片下底面的第i.,2,1,)]1([22niinRRriirOA球的体积nininRnRrVii,2,1],)1(1[232niinRRri,,2,1,)]1([22nVVVV21半球])1(21[22223nnnnR]6)12()1(1[23nnnnnnR]6)12)(1(11[23nnnR球的体积]6)12)(11(1[3nnRV半球.01,nn时当.343233RVRV从而半球334RVR的球的体积为：定理：半径是球的体积oiSo球的表面积球面被分割成n个网格，表面积分别为：则球的体积为：iV“”设小锥体的体积为iVnVVVVV321iSOO球的表面积34133RsRRSRSRSRSn31313131321RSSSSSRn31)...(31321334RVR的球的体积为：定理：半径是球的体积球的体积球的表面积球的表面积24RSR的球的表面积为：定理：半径是例4：圆柱的底面直径与高都等于球的直径.求证：（1）球的体积等于圆柱体积的（2）球的表面积等于圆柱的侧面积..32球的体积球的体积例5某街心花园有许多钢球（钢的密度是7.9g/cm3），每个...