高中数学131函数的单调性与最值课件新人教A版必修1VIP免费

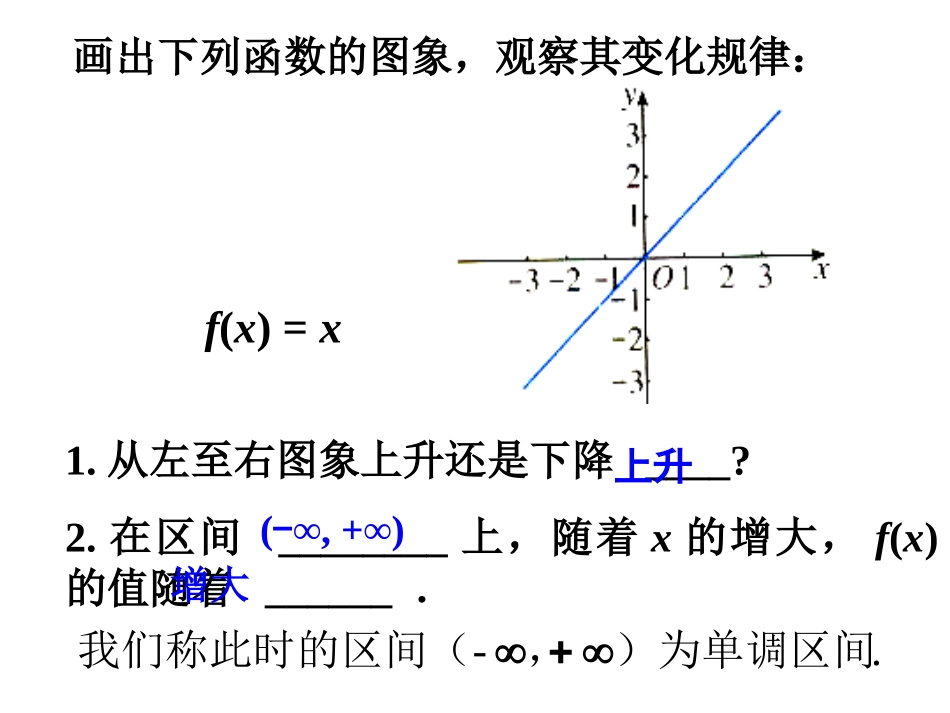
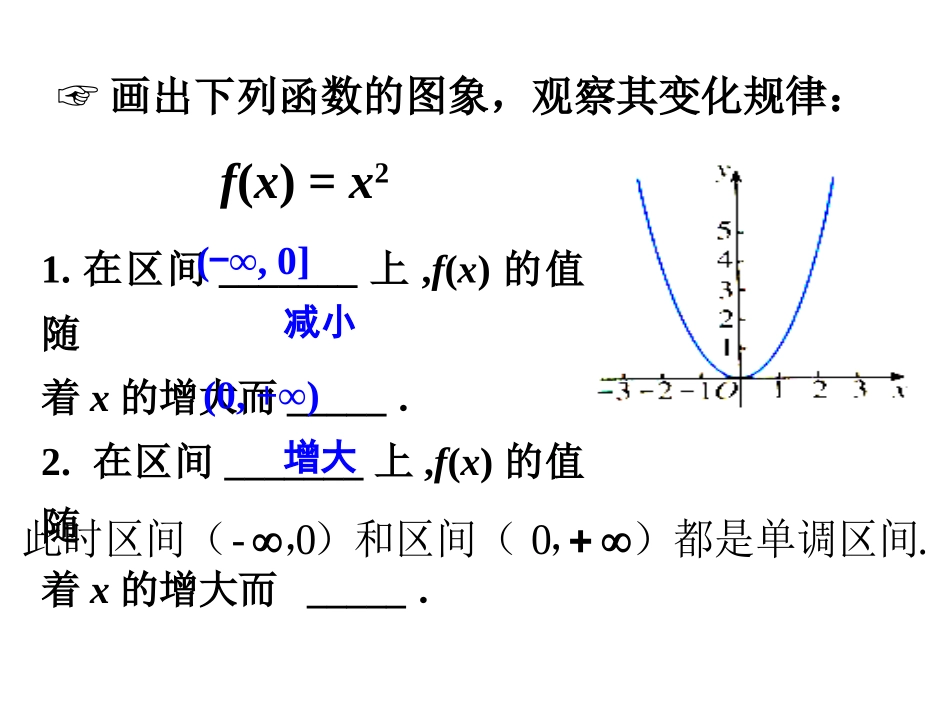
画出下列函数的图象，观察其变化规律：1.从左至右图象上升还是下降____?2.在区间________上，随着x的增大，f(x)的值随着______．f(x)=x(-∞,+∞)增大上升.-）为单调区间，我们称此时的区间（1.在区间_______上,f(x)的值随着x的增大而_____．2.在区间_______上,f(x)的值随着x的增大而_____．f(x)=x2(-∞,0](0,+∞)增大减小☞画出下列函数的图象，观察其变化规律：.00-）都是单调区间，）和区间（，此时区间（一、函数单调性定义一般地，设函数y=f(x)的定义域为I，如果对于定义域I内的某个区间D内的任意两个自变量x1，x2，当x1f(x2)）减函数例1.下图是定义在区间[-5，5]上的函数y=f(x)，根据图象说出函数的单调区间，以及在每个区间上,它是增函数还是减函数？解:函数y=f(x)的单调区间有其中y=f(x)在区间[-5,-2),[1,3)上是减函数，在区间[-2,1),[3,5]上是增函数.[-5,-2),[-2,1),[1,3),[3,5].二.典例精析区间端点问题例2.证明：函数在上是增函数.,证明：在区间上任取两个值且,12,xx12xx12xx12,,xx，且210xx23)(xxf)23()23()()(1212xxxfxf则)(312xx)()(0)()(1212xfxfxfxf即所以函数在区间上是增函数.,23)(xxf取值化简作差判号定论三、判断函数单调性的方法步骤①取值：任取x1，x2∈D，且x10，x1－1<0，x2－1<0∴f(x1)－f(x2)>0即f(x1)>f(x2)∴函数y＝x＋2x－1在[2,3]上是减函数∴f(x)的最小值为f(3)＝3＋23－1＝52.f(x)的最大值为f(2)＝2＋22－1＝4.(1)运用函数单调性求最值是求函数最值的重要方法，特别是当函数图象不好作或作不出来时，单调性几乎成为首选方法．(2)函数的最值与单调...