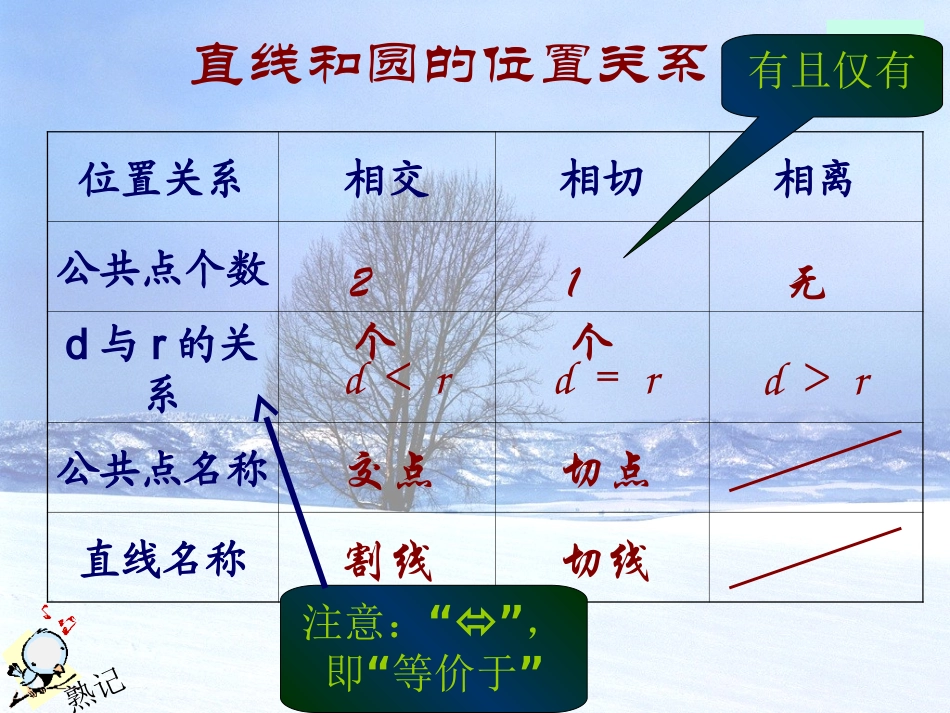
直线和圆的位置关系直线和圆的位置关系重点内容点与圆的位置关系决定因素:圆的半径为r点到圆心的距离为d三种位置关系:点在圆上d=r点在圆内d<r点在圆外d>r类比联想:直线和圆的位置关系又如何呢?温故知新直线和圆的位置关系位置关系相交相切相离公共点个数d与r的关系公共点名称直线名称2个1个无d<rd=rd>r交点切点割线切线有且仅有“注意:”,“”即等价于熟记在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?(1)r=2cm;(2)r=2.4cm;(3)r=3cm在Rt△ABC中,∠C=90°,AC=3cm,AB=5cm,以C为圆心,r为半径作圆,求r的取值范围。(1)当直线AB与⊙C相离时;(2)当直线AB与⊙C相切时;(3)当直线AB与⊙C相交时;常规题型两同心圆圆心为O,大圆的弦AB是小圆的切线,两圆的半径分别为3cm、2cm,求弦AB的长。如图,在△ABC中,∠C=90°,∠B=30°,O为AB上一点,AO=m,⊙O的半径r=0.5,问:m在什么范围内取值时,AC与⊙O(1)相离;(2)相切;(3)相交?DOABC万变不离其宗如图,直角梯形ABCD中,AD∥BC,CD=AD+BC,求证:以CD为直径的圆与AB相切。MOCDBA如图,OC⊥AB于C,∠AOC=∠B,AC=16cm,BC=4cm,求证:以8cm为半径的⊙O与AB相切。BACO切线的判定切线的判定重点内容直线和圆的位置关系d与r的关系位置关系交点个数图形lOlO2个1个无d<rd=rd>r相交相离相切熟记lO判断一条直线是不是圆的切线使用定义:直线和圆有唯一的公共点圆心到直线的距离d等于半径r时,直线和圆相切说说看:以上两种判断办法是否方便应用呢?操作:画⊙O,在⊙O上任取一点A,连结OA,过A点作直线l⊥OA直线l是否与⊙O相切呢?从作图过程看,这条切线l满足哪些条件?l经过半径外端l垂直于这条半径穷则思变切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。OCBA已知:OA=OB=5厘米,AB=8厘米,⊙O的直径6厘米。求证:AB与⊙O相切。以上两题辅助线的作法是否相同?你分析出了什么结论?辅助线技巧证明一条直线是圆的切线,常常需要作辅助线。若直线过圆上某一点,则连结圆心和公共点,再证明直线与半径垂直若直线与圆的公共点没有确定,则过圆心向直线作垂线,再证明圆心到直线的距离等于半径。相切。直线证:小圆与厘米为半径作小圆,求为圆心,以厘米,=厘米,圆内弦的半径为⊙如图,AB4O38AB8OOBA练兵如图,已知AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°,求证:DC是⊙O的切线。如图,△ABC内接于⊙O,且∠C=∠BAD,求证:AD和⊙O相切。BOCADDBACO提高切线的性质切线的性质重点内容切线判定的方法利用切线定义利用圆心到直线的距离等于半径利用切线判断定理辅助线技巧:若直线过圆上某一点,则连结圆心和公共点,再证明直线与半径垂直若直线与圆的公共点没有确定,则过圆心向直线作垂线,再证明圆心到直线的距离等于半径。Review切线判定:直线l:①过半径外端②垂直于半径切线性质:切线l,A为切点:OA⊥l理解记忆类比猜想类比猜想切线的性质定理:圆的切线垂直于经过切点的半径。推论:1、经过圆心且垂直于切线的直线必经过切点2、经过切点且垂直于切线的直线必经过圆心如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D。求证:AC平分∠DAB。综合运用DCOBAFEODCBA如图,以AD为直径的⊙O与△ABC的一边相切于D,分别交AB、AC于点E、F。求证:AE·AB=AF·AC切线判定与性质典型例题已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD。求证:DC是⊙O的切线。体会规律如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切。DCOBAFDCBAEO切线性质定理的推广性质定理:圆的切线垂直于经过切点的半径推1:经过圆心且垂直于切线的直线必经过切点推2:经过切点且垂直于切线的直线必经过圆心浓缩提炼你能用一个定理把圆的切线的性质及它的两个推论...